Etwas Galoistheorie

Dieses Kapitel ist keine  Einführung in die Galoistheorie, schon gar nicht eine leicht verständliche Einführung für ältere Schüler. Dazu fühlt sich der Autor weder berufen noch fähig. Nicht umsonst gilt die Galoistheorie, die meist im Rahmen einer Algebra-Vorlesung präsentiert wird, als sehr technisch , was sich darin zeigt, dass viele ihrer Lehrsätze mit einer langen Liste von Voraussetzungen beginnen. Will man die Lehrsätze auf einen konkreten Fall anwenden, muss man Punkt für Punkt die Gültigkeit dieser Voraussetzungen prüfen, was keineswegs immer auf Anhieb gelingt. Man beachte dazu das Zitat von Ian Stewart weiter unten.

Wie im Vorwort gesagt, dient dieses Kapitel vielmehr dazu, Lesern, die schon einmal mit der Galoistheorie in Berührung gekommen sind, die Verbindungsstellen zu dem von Gauß entwickelten Verfahren zur Auflösung der Kreisteilungsgleichung aufzuzeigen. Im Gegensatz zu den anderen Kapiteln werden hier Ergebnisse nur zitiert, ohne sie plausibel zu machen, sowie Begriffe verwendet, ohne sie zu definieren..

Wer Beweise nachlesen oder seine Kenntnisse auffrischen möchte, sei auf die einschlägige Literatur verwiesen. Neben den klassischen Lehrbüchern der Algebra gibt es mittlerweile eine Fülle von frei zugänglichen Vorlesungsskripten im Web, deren Qualität der von gedruckten Büchern nicht unbedingt nachsteht. Eine Suche mit den Schlagwörtern Algebra, Einführung, Vorlesung  oder Galoistheorie, Einführung, Vorlesung  fördert hier manches Juwel zu Tage. Speziell zur Galoistheorie ist das gleichnamige Buch [Stewart 1988] lesenswert, das zwar schon etwas älter ist, sich aber wegen seines lockeren Stils wohltuend von allzu technischen Darstellungen abhebt. Ebenfalls sehr empfehlenswert ist das Buch [Bewersdorff 2013], das bewusst für Leser ohne weitreichende Vorkenntnisse konzipiert wurde und außerdem sehr ausführlich auf die Konstruierbarkeit von regelmäßigen Vielecken eingeht.

Trotzdem seien natürlich Leser ohne entsprechendes Hintergrundwissen zur Lektüre dieses Kapitels ermutigt. Man kann sich schließlich auch über die Funktionsweise eines mp3-Players informieren, ohne jedes Detail der Komprimierungsalgorithmen zu verstehen oder von den quantenmechanischen Grundlagen eines Halbleiterspeichers gehört zu haben.

Die Galoistheorie geht auf Evariste Galois (1811-1832) zurück, dessen wildes und gewaltsam beendetes kurzes Leben ihn zu einer Art Rockstar unter den Mathematikern gemacht hat. Galois hatte entdeckt, dass die Frage, ob die Nullstellen eines Polynoms sich durch Radikale , d.h. Wurzelausdrücke darstellen lassen, beantwortet werden kann, wenn man die Symmetrien betrachtet, die diese Nullstellen aufweisen. In der modernen Darstellung sind diese Symmetrien durch eine bestimmte Gruppe, die Galoisgruppe des Polynoms, gegeben und die Polynome selbst verstecken sich hinter bestimmten Körpern, nämlich ihren Zerfällungskörpern.

Auflösbarkeit von Polynomen durch Radikale

Beginnen wir gleich mit dem, was in einer systematischen Darstellung der Theorie erst gegen Schluss kommt, dem Hauptsatz über die Auflösbarkeit von Polynomen durch Radikale:

In unserem speziellen Fall ist das Polynom $f$ natürlich \[X^n - 1 \eqndot\] Es hat Koeffizienten in dem Körper $\mathbb{Q}$ der rationalen Zahlen, der glücklicherweise die Charakteristik Null hat (d.h. $\sum^n1 \neq 0$ für alle $n \in \mathbb{N},$ wenn $0$ und $1$ die neutralen Elemente bezüglich Addition und Multiplikation in diesem Körper sind.) und wir interessieren uns nicht für irgendeine  Auflösung dieses Polynoms durch Radikale, d.h. durch Wurzeln, sondern für eine Auflösung durch ineinandergeschachtelte Quadratwurzeln.

Die Galoisgruppe ist zunächst nur für Körpererweiterungen $L:K$ und nicht für Polynome mit Koeffizienten aus $K$ definiert und zwar als Gruppe aller Automorphismen  des Körpers $L,$ die die Elemente aus $K$ unverändert lassen. Zur Erinnerung: Körperautomorphismen sind bijektive Abbildungen $\tau$ eines Körpers auf sich selbst, die die Addition und Multiplikation in diesem Körper respektieren, für die also gilt $\tau(a+b) = \tau(a)+\tau(b)$ und $\tau(ab) = \tau(a)\tau(b)$ für alle $a,b$ aus dem Körper. Was es mit der Auflösbarkeit einer Gruppe auf sich hat, braucht uns im Moment nicht zu interessieren, dazu kommen wir später.

Die Galoisgruppe eines Polynoms mit Koeffizienten in $K$ definiert man nun einfach als Galoisgruppe des Zerfällungskörpers  dieses Polynoms, d.h. des kleinsten Erweiterungskörpers von $K,$ in dem das Polynom in Linearfaktoren zerfällt. Eine Zerlegung unseres Polynoms in Linearfaktoren haben wir im Kapitel über Einheitswurzeln schon gegeben: \[X^n - 1 = (X-1)(X-\zeta)(X-\zeta^2)\cdot \dots \cdot(X-\zeta^{n-2})(X-\zeta^{n-1})\eqncomma\] wobei die $\zeta^k$ die $n$-ten Einheitswurzeln sind.

Wenn man alle diese Einheitswurzeln zu $\mathbb{Q}$ hinzunimmt, man sagt adjungiert , erhält man somit auf jeden Fall einen Körper, in dem das Polynom $X^n -1$ zerfällt, Das wäre aber mit Kanonen auf Spatzen geschossen, denn wir haben ja gesehen, dass alle Einheitswurzeln Potenzen von $\zeta$ sind. Diese Potenzen werden aber bei der Adjunktion automatisch erzeugt, weil man in dem Erweiterungskörper unbeschränkt multiplizieren darf. Es genügt demnach, die Einheitswurzel $\zeta$ zu adjungieren und man bezeichnet den dadurch entstandenen Erweiterungskörper mit $\mathbb{Q}(\zeta).$

Grad der Körpererweiterung $\mathbb{Q}(\zeta)$

Für die weiteren Überlegungen ist der Grad  der Körpererweiterung des Zerfällungskörpers (bei uns $\mathbb{Q}(\zeta)$) über dem Grundkörper (bei uns $\mathbb{Q}$) von entscheidender Bedeutung. Als Grad einer Körpererweiterung $L:K$ bezeichnet man die Dimension von $L$ über $K,$ wenn man $L$ als $K$-Vektorraum  auffasst.

Spätestens hier wird sich ein Leser, der noch nie etwas von Galoistheorie gehört hat, der Meinung anschließen, dass es sich um eine sehr technische Theorie handelt. Vielleicht hilft die Bemerkung weiter, dass man in $L,$ wenn man den Körper als $K$-Vektorraum betrachtet, einfach die Möglichkeit der Multiplikation vergisst und sich stattdessen einen möglichst kleinen Satz von Elementen aus $L$ (man nennt das die Basis  von $L$ über $K$) sucht, derart dass man jedes Element von $L$ als Linearkombination von Elementen aus der Basis mit Faktoren aus $K$ darstellen kann. Die Minimalzahl der Elemente dieser Basis ist die Dimension  des Vektorraums.

Ein wichtiger Satz der Galoistheorie besagt nun, dass der Grad einer Körpererweiterung, die durch Adjunktion eines algebraischen Elements $\rho$ an den Grundkörper $K$ entsteht, gleich dem Grad des Minimalpolynoms  von $\rho$ in $K[X]$ ist. Dabei heißt ein Element algebraisch , wenn es Nullstelle irgendeines  Polynoms aus $K[X]$ ist, was für unser $\zeta$ als Nullstelle von $X^n-1$ aus $\mathbb{Q}[X]$ jedenfalls zutrifft.

Das Minimalpolynom von $\zeta,$ d.h. das normierte Polynom kleinsten Grades, das $\zeta$ als Nullstelle hat, ist aber keineswegs $X^n-1.$ Aus der Zerlegung \[X^n - 1 = (X-1)(X-\zeta)(X-\zeta^2)\cdot \dots \cdot(X-\zeta^{n-2})(X-\zeta^{n-1})\] ergibt sich, dass $\zeta$ ebenfalls Nullstelle von \[(X-\zeta)(X-\zeta^2)\cdot \dots \cdot(X-\zeta^{n-2})(X-\zeta^{n-1})\] ist. Dieses Polynom, das wir im Kapitel über Einheitswurzeln als Kreisteilungspolynom bezeichnet hatten, hat den Grad $n-1.$

Falls $n$ eine Primzahl ist, sind wir damit fertig, denn dann ist das obige Polynom irreduzibel  und daher wirklich das Kreisteilungspolynom. Wir hatten bereits in einer Fußnote bemerkt, dass man für nicht prime $n$ nur einen Faktor dieses Polynoms als Kreisteilungspolynom bezeichnet, genauer der größten irreduziblen Faktor. Der Grund dafür wird gleich klar werden.

Wenn $n$ nicht prim ist, erzeugen die Potenzen einer Einheitswurzel $\zeta^d$ mit $d|n$ nur einen Teil des vollständigen Satzes aller Einheitswurzeln, denn es ist für $n = d\cdot k$ \[(\zeta^d)^k = \zeta^n = 1\] mit $k \lt n.$ Diese $\zeta^d$ tragen nichts zum Aufbau des Zerfällungskörpers bei. Interessant sind die zu $n$ teilerfremden Potenzen von $\zeta,$ die primitiven  Einheitswurzeln, denn diese haben die Ordnung $n,$ d.h. ihre Potenzen erzeugen alle  Einheitswurzeln.

Auf der Suche nach dem Minimalpolynom für $\zeta$ liegt es nahe, ein Polynom zu wählen, das nur diese teilerfremden Potenzen als Nullstellen hat, denn diese allein erzeugen ja schon den Zerfällungskörper. Da deren Anzahl kleiner ist als $n,$ kann man hoffen, dass dieses Polynom niedrigeren Grad hat als $n-1.$ Es liegt ebenfalls nahe, als Ansatz für das gesuchte Polynom einfach das Produkt der entsprechenden Linearfaktoren zu nehmen: \[\Phi_n = \prod_{(q,n)=1,q\leq n}(X-\zeta^q) \eqndot\] Dabei ist $(q,n)=1$ die Abkürzung für $\gcd(q,n) = 1,$ das Produkt läuft also über alle $q\leq n,$ die zu $n$ teilerfremd sind. Man muss jetzt nur  noch nachweisen, dass das Polynom $\Phi_n$ nach dem Ausmultiplizieren Koeffizienten in $\mathbb{Q}$ hat.

Es wird den Leser nicht überraschen, dass dies wirklich gelingt, die Koeffizienten liegen sogar in $\mathbb{Z}.$ Für den nicht einmal besonders komplizierten Beweis sei auf die oben erwähnte Literatur verwiesen. Dort wird ebenfalls gezeigt, dass $\Phi_n$ irreduzibel und damit das Minimalpolynom von $\zeta$ ist. $\Phi_n$ heißt $n$-tes Kreisteilungspolynom  und ist für primes $n$ mit \[(X-\zeta)(X-\zeta^2)\cdot \dots \cdot(X-\zeta^{n-2})(X-\zeta^{n-1})\] identisch.

Der Satz von Wantzel

Für alle $n$, ob prim oder nicht, wissen wir jetzt, dass der Grad der Körpererweiterung $\mathbb{Q}(\zeta)$ gleich dem Grad des Polynoms $\Phi_n$ ist, wenn $\zeta = \zeta_n$ eine $n$-te Einheitswurzel ist.

Nach Konstruktion von $\Phi_n$ ist dessen Grad aber gleich der Anzahl der zu $n$ teilerfremden natürlichen Zahlen $q$ mit $q \leq n.$ Dafür hat schon Euler eine zahlentheoretische Funktion eingeführt, die Eulersche  $\varphi$-Funktion : \[\varphi(n) = \#\{q \leq n: (q,n)=1, q,n \in \mathbb{N}\}\eqndot\] Für eine Primzahl $p$ ist $\varphi(p) = p-1,$ denn alle Zahlen $1,2,\dots,p-1$ sind zu $p$ teilerfremd.

Aber auch für Primzahlpotenzen lässt sich die Eulersche $\varphi$-Funktion relativ einfach ausrechnen, es ist \[\varphi(p^k) = p^{k-1}(p-1)\eqncomma\] denn eine Zahl $q \leq p^k$ ist genau dann teilerfremd zu $p^k,$ wenn sie kein Vielfaches von $p$ ist. Von diesen Vielfachen gibt es $p^{k-1}$ Stück, nämlich \[1p,\quad 2p,\quad 3p,\quad \dots,\quad p^{k-1}\cdot p = p^k \eqncomma\] die kleiner oder gleich $p^k$ sind, bleiben \[p^k-p^{k-1} = p^{k-1}(p-1)\] zu $p^k$ teilerfremde Zahlen kleiner oder gleich $p^k$ übrig.

Etwas schwieriger ist der Beweis, dass die Eulersche $\varphi$-Funktion multiplikativ  ist, m.a.W. dass für teilerfremde $a,b \in \mathbb{N}$ gilt \[\varphi(a\cdot b) = \varphi(a)\cdot\varphi(b)\eqncomma\] er findet sich wiederum in der erwähnten Literatur.

Aus der Multiplikativität der $\varphi$-Funktion folgt nun unmittelbar, die Darstellung für jedes $n \in \mathbb{N}$: Da $n$ eindeutig in Primfaktoren zerlegt werden kann \[n = p_1^{k_1}\cdot p_2^{k_2} \cdot \dots \cdot p_s^{k_s}\] hat man \[\varphi(n) = p_1^{k_1-1}(p_1-1) \cdot p_2^{k_2-1}(p_2-1) \cdot \dots \cdot p_s^{k_s-1}(p_s-1)\eqndot\]

Wir haben jetzt folgendes Zwischenergebnis:

Es zeigt sich, dass allein durch Betrachtung des Grads der Körpererweiterung, ohne die Galoisgruppe und deren Auflösbarkeit überhaupt zu untersuchen, ein wichtiges Ergebnis gewonnen werden kann. Dazu wenden wir uns wieder den Quadratwurzelausdrücken zu. Wir wollen ja das Polynom $X^n -1$ durch ineinandergeschachtelte Quadratwurzeln auflösen. Jede dieser Wurzeln ist Nullstelle eines quadratischen Minimalpolynoms, liegt also in einer Körpererweiterung vom Grad 2. Der Zerfällungskörper von $X^n-1$ muss daher Abschluss einer Kette von Körpererweiterungen vom Grad 2 sein. Nach der Gradformel der Galoistheorie, die ebenfalls nicht schwer zu beweisen ist, hat man einerseits \[\mathbb{Q}(\zeta) : \mathbb{Q} = \varphi(n)\] und andererseits \[\mathbb{Q}(\zeta) : \mathbb{Q} = 2^r \] mit einem geeigneten $r \in \mathbb{N}.$ Durch Gleichsetzen ergibt sich \begin{align*} 2^r &= p_1^{k_1-1}(p_1-1) \cdot p_2^{k_2-1}(p_2-1) \cdot \dots \cdot p_s^{k_s-1}(p_s-1)\eqncomma \\ 2^r &= 2^{k_1-1} \cdot p_2^{k_2-1}(p_2-1) \cdot \dots \cdot p_s^{k_s-1}(p_s-1)\eqncomma \end{align*} wenn wir die gerade Primzahl $2$ gesondert betrachten.

Damit diese Gleichung erfüllt werden kann, darf zwar der Exponent von $2$ beliebig sein (auch $0$), bei allen anderen Primfaktoren muss hingegen $p_i^{k_i-1} = 1$ gelten (sonst hätte man einen ungeraden Faktor) und $p_i-1$ muss selbst eine Zweierpotenz, $p_i$ also eine Fermatsche Primzahl sein.

Die $p_i$ stammen aber aus der Primfaktorzerlegung der Eckenzahl $n.$ Damit haben wir gezeigt, dass ein reguläres $n$-Eck nur  dann mit Zirkel und Lineal konstruierbar ist, wenn $n$ die Primfaktorzerlegung \[n = 2^k \cdot p_1 \cdot p_2 \cdot \dots \cdot p_s\] hat für lauter verschiedene Fermatsche Primzahlen $p_i.$

Das ist nichts anderes als die Umkehrung des Gaußschen Satzes über die Konstruierbarkeit von Vielecken, der, wie wir im Vorwort erwähnt haben, von Wantzel im Jahr 1837 (natürlich mit etwas anderen Methoden) bewiesen wurde. Gauß hat diesen Satz offenbar gekannt und auch einen Beweis dafür gehabt, wie man aus Hinweisen in [Gauß 1801] entnehmen kann, aber veröffentlicht hat er den Beweis nie. Ein klassischer Beweis des Satzes von Wantzel, d.h. ein Beweis ohne Galoistheorie, findet sich in [Hudson 1969].

Insbesondere sind alle regelmäßigen Vielecke mit einer Eckenzahl $p^k$ und $k>1$ nicht  konstruierbar, wenn $p$ eine ungerade Primzahl ist. Damit ist die Beschränkung auf reine Primzahlen bei den Überlegungen im Kap.4 nachträglich gerechtfertigt.

Auflösbarkeit von Gruppen

Die andere, die ursprüngliche Richtung des Gaußschen Satzes, dass jedes Vieleck mit der Eckenzahl $n = 2^k \cdot p_1 \cdot p_2 \cdot \dots \cdot p_s$ wirklich konstruierbar ist, erfordert allerdings doch Untersuchungen zur Auflösbarkeit von Gruppen. Hier kann man sich aber von vornherein auf Vielecke mit primer Eckenzahl beschränken, denn, wie wir gesehen haben, folgt aus den Konstruierbarkeit jedes $p_i$-Ecks die Konstruierbarkeit des $n$-Ecks.

Zu zeigen ist – in der Sprache der Galoistheorie, dass das Kreisteilungspolynom $\Phi_p$ für eine Fermatsche Primzahl $p$ durch quadratische Radikale auflösbar ist. Nach dem Hauptsatz zur Auflösbarkeit muss dazu die Galoisgruppe des Zerfällungskörpers von $\Phi_p$ auflösbar sein.

Eine Gruppe $G$ heißt auflösbar , wenn es eine Kette von Untergruppen \[I = G_0 \subseteq G_1 \subseteq \dots \subseteq G_s = G\] gibt mit $G_i \lhd G_{i+1}$ für $i = 0,1, \dots , s-1$ und die Faktorgruppe $G_{i+1}/G_i$ jeweils abelsch ist. Das Symbol $G_i \lhd G_{i+1}$ bedeutet dabei, dass $G_i$ nicht nur Untergruppe sondern sogar Normalteiler  in $G_{i+1}$ ist.

Das ist nun wieder eine der typischen, abschreckend technischen Definitionen. Wir müssen jedoch gar nicht genau wissen, was dies im Einzelnen bedeutet, denn es lässt sich ganz generell beweisen, dass für Primzahlen $p$ jede Gruppe mit $p^k$ Elementen (man sagt, die Gruppe habe die Ordnung  $p^k$) auflösbar ist. Dabei gilt sogar, dass die Normalteiler $G_i$ aus der Kette jeweils die Ordnung $p^i$ haben.

Und nun kommt das schwerste Geschütz, das die Galoistheorie zu bieten hat, nämlich ihr Hauptsatz (nicht zu verwechseln mit dem Hauptsatz über die Auflösbarkeit eines Polynoms durch Radikale):

Wiederum ist es sicher keine Überraschung, dass man für die Körpererweiterung $\Phi_p : \mathbb{Q}$ die erforderlichen Eigenschaften Endlichkeit, Separabilität und Normalität nachweisen kann (als bequeme, wenn auch etwas missbräuchliche Schreibweise haben wir den Zerfällungskörper von $\Phi_p$ ebenfalls mit $\Phi_p$ bezeichnet). Die Körpererweiterung hat nach Voraussetzung den Grad $2^k.$ Also hat die Galoisgruppe dieser Erweiterung die Ordnung $2^k$ und ist somit – als Gruppe von Primzahlpotenzordnung – auflösbar.

Es gibt demnach in der Galoisgruppe eine Kette von Normalteilern $G_i,$ von denen jeder die Ordnung $2^i$ hat. Es gibt somit die entsprechende Kette von Zwischenkörpern \[\mathbb{Q} = G_s^\dagger \subseteq G_{s-1}^\dagger \subseteq \dots \subseteq G_1^\dagger \subseteq G_0^\dagger = \Phi_p\] und der Grad der Körpererweiterung $\Phi_p : G_i^\dagger$ ist $2^i.$ Der Grad der Körpererweiterung $G_i^\dagger : G_{i+1}^\dagger$ muss daher $2$ sein und $G_{i}^\dagger$ ist mithin Zerfällungskörper eines Polynoms vom Grad $2$ mit Koeffizienten aus $G_{i+1}^\dagger.$ Das ist aber genau das, was wir zeigen wollten.

Wo sind die Gaußschen Perioden geblieben?

In den Überlegungen, die wir bisher angestellt haben, zeigt sich die ganze Stärke, aber auch die Problematik der Galoistheorie. Wir haben das Gaußsche und das Wantzelsche Resultat abgeleitet, ohne einen konkreten Hinweis zu bekommen, wie nun tatsächlich die Minimalpolynome der Erweiterungen $G_{i}^\dagger : G_{i+1}^\dagger$ bestimmt werden und wie die adjungierten Wurzeln tatsächlich aussehen. Das ist keineswegs untypisch für die Galoistheorie. Ian Stewart schreibt etwa in [Stewart 1988]:

[…] it is necessary to compute the corresponding Galois group. This is far from being a simple or straightforward task, and until now we have strenuously avoided it.

Glücklicherweise ist das Polynom $X^p -1$ besonders einfach. Es ist sogar das einfachste nicht triviale Polynom $p$-ten Grades überhaupt. Die Galoisgruppe für die zu diesem Polynom gehörende Körpererweiterung sollte daher ebenfalls eine einfache Struktur haben.

Wir erinnern uns, dass die Galoisgruppe von $\mathbb{Q}(\zeta) : \mathbb{Q},$ die wir von jetzt an mit $\Gamma$ bezeichnen wollen, aus allen Automorphismen $\tau$ von $\mathbb{Q}(\zeta)$ besteht, die die Elemente von $\mathbb{Q},$ also die rationalen Zahlen, unverändert lassen. Da jeder Automorphismus die Multiplikation in $\mathbb{Q}(\zeta)$ respektiert, ist $\tau$ folglich allein durch seine Wirkung auf die eine  Einheitswurzel $\zeta$ vollständig bestimmt.

$\tau$ kann aber $\zeta$ nicht auf ein Element $a$ aus $\mathbb{Q}$ abbilden, denn als Automorphismus ist $\tau$ insbesondere injektiv und es gilt ja schon $\tau(a) = a.$ Es bleibt für $\tau$ demnach gar keine andere Möglichkeit, als $\zeta$ auf eine andere $p$-te Einheitswurzel abzubilden, die, wie wir gesehen haben, durch Adjunktion von $\zeta$ automatisch in $\mathbb{Q}(\zeta)$ mit erzeugt werden. Jede dieser Einheitswurzeln ist aber eine Potenz von $\zeta,$ also gilt \[\tau(\zeta) =\zeta^\omega\] mit einem $\omega \in \mathbb{N}$ und dadurch ist der Automorphismus $\tau$ vollständig bestimmt.

Die Gruppenoperation in einer Automorphismengruppe ist nun nichts anderes als die Hintereinanderausführung der Automorphismen. Wenden wir also $\tau$ mehrfach auf $\zeta$ an: $$ \begin{align*} \tau(\zeta) &= \zeta^\omega \\ \tau^2(\zeta) = \tau(\tau(\zeta)) &= (\zeta^\omega)^\omega = \zeta^{\omega^2} \\ \tau^3(\zeta) = \tau(\tau^2(\zeta)) &= (\zeta^{\omega^2})^\omega = \zeta^{\omega^3} \\ & \text{usw.} \\ \end{align*} $$ Da tauchen sie wieder auf, die Summanden der Gaußschen Perioden, wobei wir durch die Bezeichnung $\omega$ für den Exponenten etwas nachgeholfen haben.

Mit $\omega$ hatten wir das primitive Element in $\mathbb{Z}/p\mathbb{Z}$ bezeichnet und wenn man in der obigen Definition von $\tau$ den Exponenten $\omega$ als primitives Element wählt, erzeugt $\tau$ die gesamte Galoisgruppe $\Gamma,$ denn jeder Exponent von $\zeta$ lässt sich als $\omega^k$ mit einem geeigneten $k$ schreiben und jeder Automorphismus aus $\Gamma$ muss $\zeta$ auf eine Potenz von $\zeta$ abbilden, also von der Form $\tau^k$ sein.

Eine Gruppe, die von einem Element $\tau$ erzeugt wird, nennt man zyklische  Gruppe und bezeichnet sie üblicherweise mit $\langle \tau \rangle.$ Es ist also $\Gamma = \langle \tau \rangle,$ wenn $\tau$ wie oben definiert wird. Man kann sich nun leicht davon überzeugen, dass auch $\tau^2, \tau^4$ usw. Gruppen erzeugen und zwar Untergruppen von $\Gamma,$ für die gilt \[\Gamma = \langle \tau \rangle \supset \langle \tau^2 \rangle \supset \langle \tau^4 \rangle \supset \dots \supset \langle \tau^{p-1/2} \rangle \supset \langle \tau^{p-1} \rangle = 1\] und weil zyklische Gruppen abelsch sind, sind alle Untergruppen automatisch Normalteiler \[\langle \tau^{2^k} \rangle \lhd \langle \tau^{2^{k-1}} \rangle\] und die Faktorgruppen sind ebenfalls abelsch, so dass wir tatsächlich die Auflösung der Galoisgruppe $\Gamma$ gefunden haben.

Nach dem Hauptsatz der Galoistheorie kennen wir damit ebenfalls die zugehörige Kette von Körpererweiterungen: \[\mathbb{Q} = {\langle \tau \rangle}^\dagger \subset {\langle \tau^2 \rangle}^\dagger \subset {\langle \tau^4 \rangle}^\dagger \subset \dots \subset {\langle \tau^{p-1/2} \rangle}^\dagger \subset {\langle \tau^{p-1} \rangle}^\dagger = \mathbb{Q}(\zeta)\] wobei die Elemente der Zwischenkörper ${\langle \tau^{k} \rangle}^\dagger$ jeweils von den Automorphismen von $\langle \tau^{k} \rangle$ unverändert gelassen werden. Die Zwischenkörper sind demnach Fixkörper  für die Automorphismen aus den entsprechenden Untergruppen. Außerdem ergibt sich aus den diversen Gradsätzen der Galoistheorie, dass jede der Körpererweiterungen in der Kette der Fixkörper den Grad $2$ hat.

Für das primitive Element $\omega$ können wir wieder eine spezielle Wahl treffen. Wir bleiben bei der klassischen $3$ und betrachten, wie mehrfache Anwendung von $\tau$ auf $\zeta$ wirkt:

\[ \require{AMScd} \begin{CD} \zeta @>\tau>> \zeta^3 @>\tau>> \zeta^{3^2} @>\tau>> \zeta^{3^3} @>\tau>> \dots \end{CD} \]

alles natürlich$\pmod{p}$ betrachtet. Berücksichtigt man jetzt noch, dass \[\tau(\zeta^{3^{p-2}}) = \zeta^{3^{p-1}} = \zeta\] ist, sieht man gleich, dass $\tau$ die $0$-te Gaußsche Periode \[\zeta + \zeta^3 + \zeta^{3^2} + \dots + \zeta^{3^{p-2}}\] auf sich selbst abbildet – jeder Summand rutscht unter $\tau$ eine Position nach rechts und der letzte an Position $1.$ Für die $0$-te Periode ist das kein Wunder, denn diese hat den Wert $-1,$ liegt also in $\mathbb{Q}$ und alle Automorphismen der Galoisgruppe haben den Fixkörper $\mathbb{Q}.$

Das Argument gilt ebenso für Potenzen von $\tau,$ z. B. für $\tau^2$:

\[ \begin{CD} \zeta @>\tau^2>> \zeta^{3^2} @>\tau^2>> \zeta^{3^4} @>\tau^2>> \zeta^{3^6} @>\tau^2>> \dots \end{CD} \] \[ \begin{CD} \zeta^3 @>\tau^2>> \zeta^{3^3} @>\tau^2>> \zeta^{3^5} @>\tau^2>> \zeta^{3^7} @>\tau^2>> \dots \end{CD} \]

und wir sehen, dass $\tau^2$ die beiden Gaußschen Perioden der Stufe $1$ unverändert lässt. Die Konstruktion der Perioden ist gerade so gewählt, dass dies für alle  Potenzen von $\tau$ und die Perioden der entsprechenden Stufe gilt. Die Gaußschen Perioden $k$-ter Stufe liegen also im Fixkörper ${\langle \tau^{2^k} \rangle}^\dagger.$ Darüberhinaus lässt sich sogar zeigen (siehe [Tijsma 2016]), dass jede Gaußsche Periode $k$-ter Stufe den Fixkörper erzeugt, dass also gilt $$ {\langle \tau^{2^k} \rangle}^\dagger = \mathbb{Q}(p_{k,m}) $$ für eine beliebige Periode $p_{k,m}$ der Stufe $k.$

Überraschenderweise lässt sich auf diesem abstrakten Niveau unsere Aussage über das Produkt Gaußscher Perioden, dessen Beweis uns in Kap. 5 ja einige Mühe gekostet hat, völlig zwanglos, ohne Rechnerei und fast anschaulich ableiten. Wir betrachten dazu eine Periode der Stufe $n-1$ unter $\tau^{2^{n-1}},$ das wir zur Abkürzung mit $\tau^*$ bezeichnen.

$$ \newcommand{\opow}[1]{\omega^{#1}} $$ \[ \begin{CD} \zeta^{\opow{s}} @>\tau^*>> \zeta^{\opow{s+n-1}} @>\tau^*>> \zeta^{\opow{s+2(n-1)}} @>\tau^*>> \zeta^{\opow{s+3(n-1)}} @>\tau^*>> \dots \end{CD} \]

wobei wir mit irgendeiner passenden Potenz $\zeta^{\opow{s}}$ des primitiven Elements $\omega$ beginnen. Die Periode wird, wie wir soeben gesehen haben, auf sich selbst abgebildet. Wenn man diese Periode nach den bekannten Regeln in zwei Perioden der Stufe $n$ aufteilt, hat man^[1]:

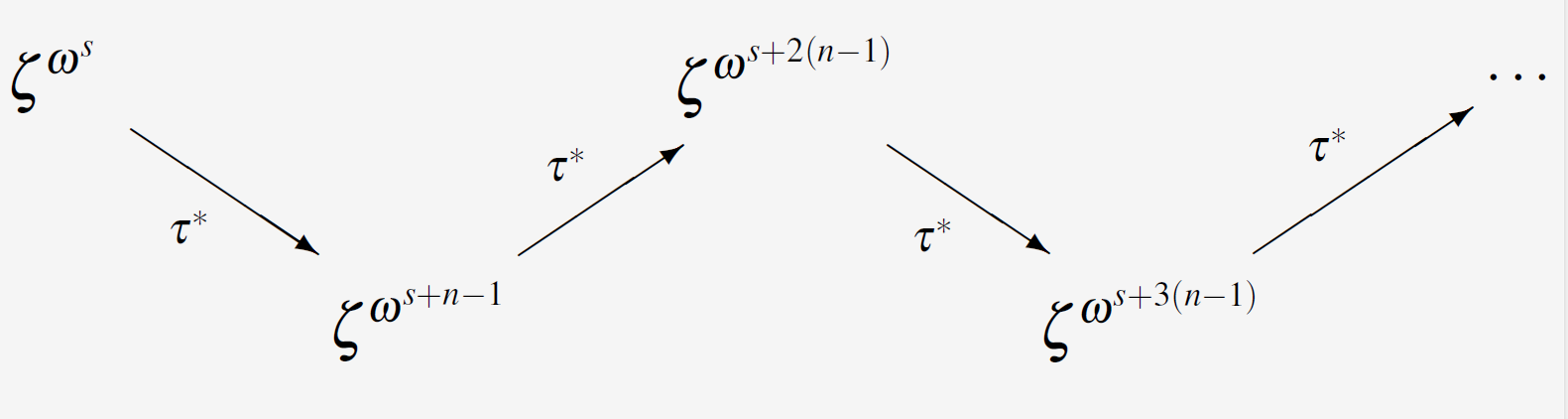
und man sieht sofort, dass $\tau^*$ die beiden durch Aufspaltung erzeugten Perioden vertauscht. Wenn wir die obere der beiden Perioden in dem Diagramm mit $p_{n,m}$ bezeichnen und die untere mit $p_{n,m+2^{n-1}}$ gilt für das Produkt:

$$ \begin{align*} \tau^*(p_{n,m}\cdot p_{n,m+2^{n-1}}) &= \tau^*(p_{n,m})\cdot\tau^*( p_{n,m+2^{n-1}}) \\ &= p_{n,m+2^{n-1}} \cdot p_{n,m} \\ &= p_{n,m}\cdot p_{n,m+2^{n-1}} \eqndot \end{align*} $$

Daher liegt das Produkt der beiden durch Aufspaltung erzeugten Perioden der Stufe $n$ in ${\langle \tau^* \rangle}^\dagger,$ d.h. im Fixkörper des Automorphismus $\tau^{2^{n-1}}.$ Dieser Fixkörper wurde aber durch Adjunktion der Perioden der Stufe $n-1$ erzeugt, folglich ist das Produkt der beiden Perioden der Stufe $n$ ein rationaler Ausdruck mit Perioden der Stufe $n-1.$

Für die Aufstellung der quadratischen Gleichung, die die beiden Perioden als Nullstellen hat, genügt bereits diese Aussage. Dass der rationale Ausdruck sogar eine Linearkombination ist, erfordert einige zusätzliche Überlegungen.

Schlussbemerkung

Das soll für einen Exkurs über Galoistheorie genügen. Wir haben unsere Gaußschen Perioden wiedergefunden. Sie stammen aus den Fixkörpern zwischen $\mathbb{Q}$ und $\mathbb{Q}(\zeta),$ die sich aus der Auflösung der Galoisgruppe dieser Körpererweiterung zwangsläufig ergeben. Wir haben daraus sogar einen anschaulichen Beweis für die Darstellung des Produkts zweier durch Aufspaltung erzeugter Perioden gewonnen.

Es sei noch bemerkt, dass Gaußsche Perioden ein Spezialfall der Gaußschen Summen sind. Es empfiehlt sich also, nach diesem Stichwort zu suchen, wenn man, um Gauß das letzte Wort zu geben, mehr über den Zusammenhang der Wurzeln untereinander nach arithmetischen Gründen lernen möchte.