Einheitswurzeln

Besonders einfach wird die Multiplikationsregel für komplexe Zahlen vom Betrag Eins . Dann entfällt die Streckung und man muss lediglich die Argumente (Polarwinkel) addieren, hat also eine reine Drehung.

Wir erinnern uns, dass der Betrag einer komplexen Zahl als ihr Abstand vom Ursprung definiert ist. Komplexe Zahlen gleichen Betrags liegen demnach auf einem Kreis um den Ursprung, dessen Radius gleich diesem Betrag ist. Speziell für komplexe Zahlen vom Betrag Eins ist dies der Kreis mit Radius $1$ um den Ursprung, der Einheitskreis .

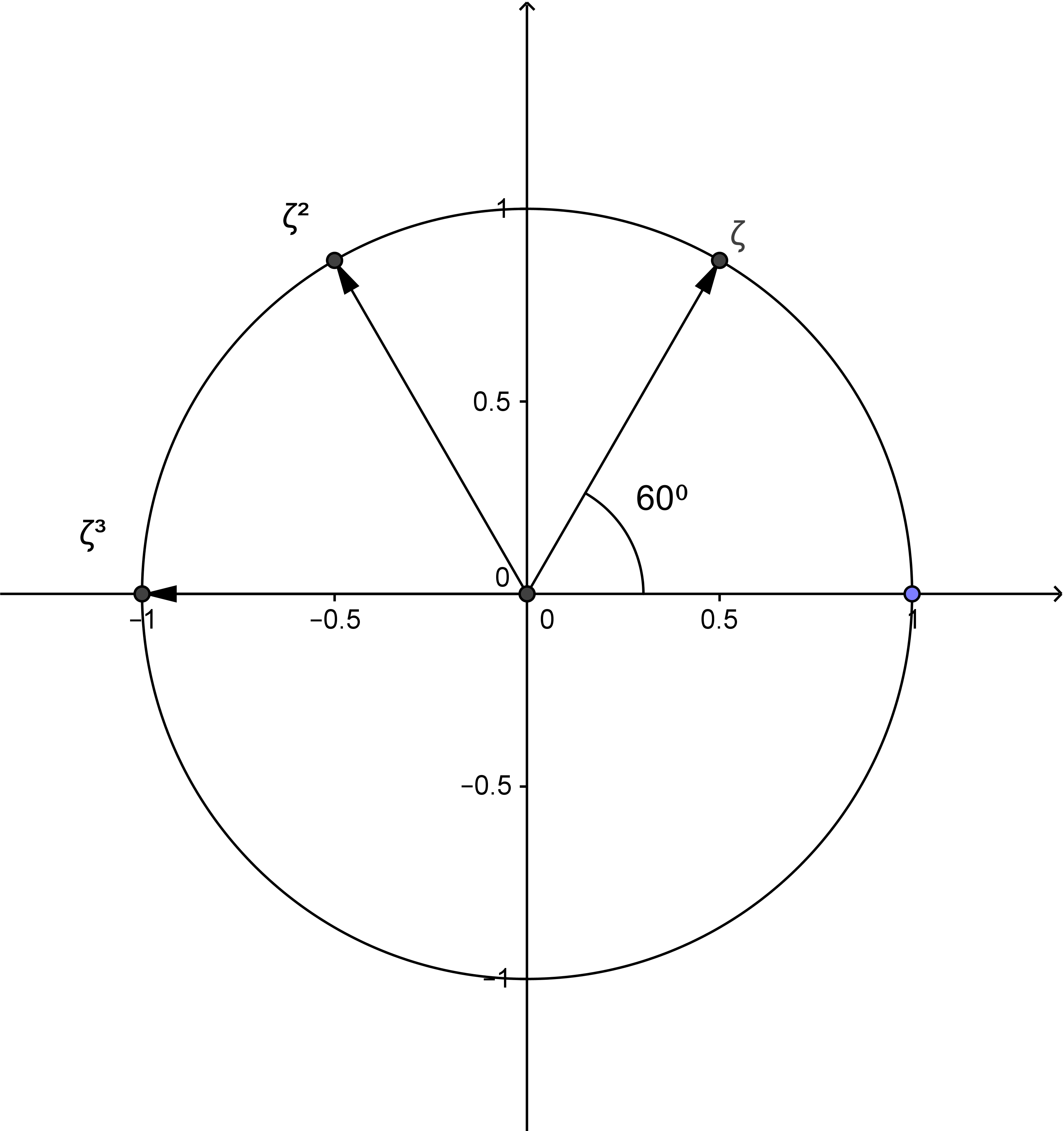
Betrachtet man etwa eine komplexe Zahl $\zeta$ mit $|\zeta| = 1$ und nimmt an, dass ihr Polarwinkel 60° beträgt (siehe Abb.1), so erhält man durch Multiplikation $\zeta \cdot \zeta$ die komplexe Zahl $\zeta^2,$ deren Betrag ebenfalls $1$ ist, und deren Polarwinkel 120° ist. Eine weitere Multiplikation mit $\zeta$ liefert $\zeta^3$ mit dem Polarwinkel 180° usw.

Durch fortlaufende Multiplikation ergibt sich folgende Tabelle in Polarkoordinaten, aus der man erkennt, dass die komplexen Zahlen $\zeta,\dots,\zeta^6$ auf dem Einheitskreis gleichmäßig verteilt liegen, und somit ein regelmäßiges Sechseck  bilden: $$ \begin{align*} \zeta = \zeta^1 &= (1,60^{\circ}) \\ \zeta^2 &= (1,120^{\circ})\\ \zeta^3 &= (1,180^{\circ}) \\ \zeta^4 &= (1,240^{\circ}) \\ \zeta^5 &= (1,300^{\circ}) \\ \zeta^6 &= (1,360^{\circ}) = (1,0^{\circ}) = \zeta^0 \\ \zeta^7 &= (1,420^{\circ}) = (1,60^{\circ})= \zeta \\ \end{align*} $$

Aus der obigen Tabelle entnimmt man, dass $(\zeta^1)^6 = \zeta^6 = (1,0^{\circ}) = 1$ gilt. Aber auch alle anderen Potenzen von $\zeta$ ergeben den Wert $1,$ wenn man sie nochmals mit $6$ potenziert: \[(\zeta^k)^6 = \zeta^{k\cdot6} = \zeta^{6\cdot k} = (\zeta^6)^k = 1^k = 1\eqndot\] Eine Zahl, die mit $6$ potenziert den Wert $1$ ergibt, nennt man bekanntlich 6te Wurzel aus $1,$ oder kurz 6te Einheitswurzel . Die obige Tabelle zeigt die sechs verschiedenen komplexen 6ten Einheitswurzeln und man sieht, dass diese genau die Eckpunkte eines regelmäßigen Sechsecks bilden.

Regelmäßige $n$-Ecke

Was oben für das Sechseck durchgeführt wurde, gilt für jedes regelmäßige Vieleck, wenn dessen Umkreis den Radius 1 hat. Im regelmäßigen $n$-Eck ist der Winkel zwischen benchbarten Radii vom Mittelpunkt zu den einzelnen Ecken $360^{\circ}/n.$ Wir wollen im Folgenden die Winkel nicht mehr in Grad messen, sondern im Bogenmaß, d.h. durch die Länge des Kreisbogens, der von den Schenkeln des Winkels aus einem Kreis mit Radius 1 um den Scheitelpunkt ausgeschnitten wird. Es gilt $360^{\circ} \hateq 2\pi,$ $180^{\circ} \hateq \pi,$ $90^{\circ}\hateq \pi/2$ usw.

Üblicherweise zählt man die Ecken eines regelmäßigen Vielecks gegen den Uhrzeigersinn und beginnt bei $\zeta^0 = 1,$ der Ecke, die auf der $x$-Achse liegt. Die nächste Ecke $\zeta^1=\zeta$ entspricht der komplexen Zahl \[cos(2\pi/n) + \I\sin(2\pi/n) = e^{\frac{2\pi\I}{n}}\] und für die $k$-te Ecke hat man \[\zeta^k = (e^{\frac{2\pi\I}{n}})^k = e^{\frac{2\pi\I k}{n}}\eqndot\] Man beachte, dass bei dieser Art der Nummerierung $k$ nicht nur ein Index ist, sondern wirklich der Exponent, mit dem $\zeta^1 = \zeta$ zu potenzieren ist, um die $k$-te Ecke $\zeta^k$ als komplexe Zahl zu erhalten. Dass jede dieser komplexen Zahlen tatsächlich eine $n$-te Einheitswurzel ist, ergibt sich sofort aus den Eigenschaften der Exponentialfunktion: $$ \begin{align*} (\zeta^k)^n &= (e^{\frac{2\pi\I k}{n}})^n \\ &= e^{\frac{2\pi\I kn}{n}} \\ &= e^{2\pi\I k} = (e^{\I\pi})^{2k} = (-1)^{2k} = 1 \eqncomma\\ \end{align*} $$ wobei der Spezialfall der Eulerschen Identität  für $\varphi = \pi$ benutzt wurde: \[e^{\I\pi} = \cos\pi + \I\sin\pi = -1\eqndot\] An dieser Stelle darf natürlich keinesfalls der Hinweis fehlen, dass diese Gleichung von vielen Mathematikern für die schönste  der gesamten Mathematik gehalten wird, insbesondere, wenn man sie in der Form \[e^{\I\pi} + 1 = 0\] schreibt, weil die wichtigsten Konstanten der Mathematik $e, \pi, \I, 1$ und $0$ hier in nicht trivialer Weise verknüpft sind.

Aber zurück zur Konstruktion regelmäßiger Vielecke. Wir wollen das Ergebnis der bisherigen Überlegungen in kompakter Form festhalten:

Wenn wir ein festes $n$-Eck betrachten, oder wenn es auf die Eckenzahl nicht ankommt, lassen wir, wie oben schon praktiziert, den Index $n$ bei $\zeta_n^k$ weg und schreiben kurz $\zeta^k.$

Das Kreisteilungspolynom

Die $n$-ten Einheitswurzeln sind Lösungen der Gleichung $x^n = 1$ mit $x \in \mathbb{C}$ oder, anders ausgedrückt, die komplexen Nullstellen des Polynoms $X^n-1.$ Wir halten uns hier an die Konvention, die Unbekannte in einem Polynom mit Großbuchstaben zu schreiben. Diese Schreibweise erinnert daran, dass man mit Polynomen genau so rechnen kann, wie mit ganzen Zahlen, sie also beliebig addieren, subtrahieren und multiplizieren kann. Man sagt, dass die Polynome einen Ring  bilden, den man mit $\mathbb{Q}[X]$ oder mit $\mathbb{Z}[X]$ bezeichnet, je nachdem ob die Koeffizienten^[1] des Polynoms aus $\mathbb{Q}$ oder aus $\mathbb{Z}$ stammen.

Eine Nullstelle des Polynoms $X^n-1$ kann man unabhängig von $n$ sofort angeben, nämlich $\zeta^0=1.$ In dem Polynom $X^n-1$ lässt sich daher der lineare Faktor $X-1$ herausdividieren und man hat: \[X^n-1 = (X-1)(X^{n-1} + X^{n-2} + \dots + X^2 + X + 1)\eqndot\] Die Richtigkeit dieser Gleichung kann man einfach durch Ausmultiplizieren nachweisen. Den zweiten Faktor, also den Ausdruck $X^{n-1}+X^{n-2}+\dots+X^2+X+1$ bezeichnet man als Kreisteilungspolynom ^[2], denn es sind die Nullstellen dieses  Polynoms, die für die Konstruktion des regelmäßigen $n$-Ecks relevant sind, die triviale Nullstelle $\zeta^0 = 1$ ist ja ohnehin vorgegeben.

Das Kreisteilungspolynom ist folglich nicht  das Polynom $X^n-1,$ obwohl man die Gleichung $x^n=1$ oder $x^n-1=0$ für komplexes $x$ durchaus manchmal als Kreisteilungsgleichung  bezeichnet. Die Begriffe bezeichnen natürlich nahe Verwandtes, trotzdem sollte man sie nicht verwechseln.

Es sei gleich noch ein Ergebnis festgehalten, das später eine wichtige Rolle spielen wird. Aus der obigen Produktdarstellung ergibt sich nämlich: \[X^{n-1}+X^{n-2} +\dots+X^2+X+1 = \frac{X^n-1}{X-1}\eqndot\] Setzt man hier die $n$-te Einheitswurzel $\zeta = \zeta^1$ ein, hat man \[\zeta^{n-1}+\zeta^{n-2}+\dots+\zeta^2+\zeta=\frac{\zeta^n-1}{\zeta-1}-1=\frac{1-1}{\zeta-1}-1=-1\eqndot\]

Das lässt sich geometrisch veranschaulichen: Wir betrachten dazu wieder das regelmäßige Sechseck. Aus Symmetriegründen ist mit jeder Ecke $\zeta$ eines regelmäßigen Vielecks die zugehörige konjugiert komplexe Zahl $\bar{\zeta}$ ebenfalls eine Ecke (siehe Abb.2). Nach der üblichen Nummerierung ist $\overline{\zeta^k}=\zeta^{n-k}=\zeta^{-k}.$ Wenn $n$ gerade ist, gilt insbesondere für $k = n/2,$ dass $\overline{\zeta^{n/2}} = \zeta^{n/2}.$ Das trifft bei der Ecke $-1$ zu, die zu sich selbst konjugiert komplex ist.

In der obige Summe kommen alle Einheitswurzeln bis auf 1 vor, die Summe lässt sich so umsortieren, dass immer eine Einheitswurzel mit ihrem konjugiert komplexen zusammengefasst wird. Für jede komplexe Zahl ist aber $\zeta+\overline{\zeta}$ reell und wiederum aus Symmetriegründen ist im Sechseck $\zeta^1+\zeta^5 = - (\zeta^2+\zeta^4),$ so dass von der Summe nur der zu sich selbst konjugiert komplexe Wert $\zeta^3 = -1$ übrig bleibt.

Für ungerade Vielecke ist die geometrische Veranschaulichung nicht ganz so suggestiv, da es keine Ecke $-1$ gibt und die Ecken zwar symmetrisch zur reellen Achse liegen aber nicht zur imaginären. Trotzdem gibt es sozusagen ein physikalisches Argument, das die soeben abgeleitete Identität anschaulich klar macht: Wenn man die komplexen Einheitswurzeln als Vektoren auffasst, nämlich als Kraftvektoren, die am Ursprung ansetzen, ist die auf den Ursprung wirkende Nettokraft gleich Null, da dieser gleichmäßig nach allen Seiten gezerrt wird. Betrachtet man speziell den Vektor vom Ursprung zum Punkt $1,$ so muss dessen Kraftwirkung durch die Summe der Kräfte aller übrigen Vektoren kompensiert werden und das heißt gerade, dass die Summe der Einheitswurzeln ohne die $1$ genau $-1$ ergeben muss.

Elementarsymmetrische Ausdrücke

Eine weitere Möglichkeit, die Summe der Einheitswurzeln zu berechnen, soll hier ebenfalls noch erwähnt werden, weil die Methode später in anderem Zusammenhang verwendet wird und weil sich sozusagen nebenbei noch Aussagen über (wie Gauß es ausdrückte) den Zusammenhang der Wurzeln untereinander nach arithmetischen Gründen  ergeben.

Das Kreisteilungspolynom $X^{n-1}+X^{n-2} +\dots+X^2+X+1$ hat als Nullstellen die Einheitswurzeln $\zeta, \zeta^2, \dots ,\zeta^{n-1},$ es zerfällt also über den komplexen Zahlen in Linearfaktoren: \[X^{n-1}+X^{n-2} +\dots+X^2+X+1 = (X-\zeta)(X-\zeta^2)\cdot \dots \cdot(X-\zeta^{n-2})(X-\zeta^{n-1})\eqndot\] Die rechte Seite kann man ausmultiplizieren und nach Potenzen von $X$ sortieren. Für $X^{n-1}$ nimmt man aus jeder Klammer den Wert $X$ und keines der $\zeta^k,$ der Koeffizient $1$ bei $X^{n-1}$ ergibt sich damit automatisch.

Für $X^{n-2}$ nimmt man aus $n-2$ Klammern den Wert $X$ und aus einer den Wert $\zeta^k,$ jeweils für jedes $\zeta^k,$ so dass man den Koeffizienten $-\zeta-\zeta^2-\dots-\zeta^{n-1}$ für $X^{n-2}$ erhält. Für $X^{n-3}$ nimmt man aus jeder Klammer bis auf zwei den Wert $X$ und aus zwei Klammern jeweils den Wert $\zeta^k$ bzw. $\zeta^l.$ Der Koeffizient von $X^{n-3}$ ist somit die Summe aller möglichen Produkte von zwei  unterschiedlichen Einheitswurzeln: $\zeta\zeta^2 + \zeta\zeta^3 + \dots + \zeta^{n-2}\zeta^{n-1}.$

So kann man jeden Koeffizienten einer Potenz von $X$ ausrechnen und erhält für die Konstante 1 schließlich das Produkt $\pm\zeta\zeta^2\cdot\dots\cdot\zeta^{n-2}\zeta^{n-1},$ wobei das Vorzeichen davon abhängt, ob $n-1$ gerade oder ungerade ist.

Man nennt die so ausmultiplizierten Koeffizienten, jeweils mit positivem Vorzeichen versehen, die elementarsymmetrischen Ausdrücke  in den $\zeta,\zeta^2,\dots,\zeta^{n-1}.$ Der Name kommt daher, weil man in den Koeffizienten jede Einheitswurzel $\zeta^k$ mit jeder anderen $\zeta^l$ vertauschen darf, ohne am Wert des Ausdrucks etwas zu ändern. Die Koeffizienten sind also invariant  gegenüber allen Permutationen  der Einheitswurzeln, verhalten sich m.a.W. bezüglich dieser Permutationen symmetrisch .

Durch Vergleich mit den Koeffizienten des Kreisteilungspolynoms erhält man wieder die bekannte Summenformel für die Einheitswurzeln, denn der Koeffizient von $X^{n-2}$ ist einerseits $1$ und andererseits $-\zeta-\zeta^2-\dots-\zeta^{n-1}.$

Da alle Koeffizienten des Kreisteilungspolynoms gleich $1$ sind, ergibt sich durch Koeffizientenvergleich ganz allgemein, dass alle  elementarsymmetrischen Ausdrücke in den Einheitswurzeln den Wert $\pm1$ haben.

Für die Einheitswurzeln lassen sich die elementarsymmetrischen Ausdrücke natürlich leicht vereinfachen, so dass man annehmen könnte, dass wir hier mit viel Aufwand eine Trivialität bewiesen haben. Beispielsweise gilt für das konstante Glied: \[\zeta\zeta^2\cdot\dots\cdot\zeta^{n-2}\zeta^{n-1} = (\zeta\zeta^{n-1})(\zeta^2\zeta^{n-2})\dots\eqncomma\] so dass wir bei ungeradem $n$ lauter Faktoren $\zeta^n=1$ bekommen, mithin das Multiplikationsergebnis $+1.$ Bei geradem $n$ bleibt ein Faktor $\zeta^{n/2}$ übrig, der ist aber gerade^[3] gleich $-1,$ wie wir schon beim Sechseck gesehen haben.

Bleiben wir beim Sechseck und vergleichen wir hier den Koeffizienten von $X^{n-3}$: $$ \begin{align*} 1 &= \zeta\zeta^2 +\zeta\zeta^3+\zeta\zeta^4+\zeta\zeta^5+\zeta^2\zeta^3+\zeta^2\zeta^4+\zeta^2\zeta^5+\zeta^3\zeta^4+\zeta^3\zeta^5+\zeta^4\zeta^5\\ &= \zeta^3+\zeta^4+\zeta^5+\zeta^6+\zeta^5+\zeta^6+\zeta^7+\zeta^7+\zeta^8+\zeta^9\\ &= \zeta^3+\zeta^4+\zeta^5+1+\zeta^5+1+\zeta+\zeta+\zeta^2+\zeta^3\\ &= 2(1+\zeta+\zeta^3+\zeta^5)+(\zeta^2+\zeta^4)\\ &= 2(\zeta+\zeta^5)+(\zeta^2+\zeta^4) \end{align*} $$ In der vorletzten Zeile haben wir für $\zeta^3$ den Wert $-1$ eingesetzt. Hier liefert der Koeffizientenvergleich keine Trivialität sondern immerhin einen geometrischen Zusammenhang, den man bei aufmerksamem Betrachten der Abb.2 bestätigt findet.

Zusammen mit dem Ergebnis aus dem Koeffizientenvergleich für $X^{n-2}$ erhält man ein System von zwei Gleichungen für die beiden Unbekannten $\zeta+\zeta^5$ und $\zeta^2+\zeta^4$: $$ \begin{align*} 2(\zeta+\zeta^5)+(\zeta^2+\zeta^4) &= 1\\ (\zeta+\zeta^5) + (\zeta^2+\zeta^4) &= 0\\ \end{align*} $$ Die zweite Gleichung ergibt sich aus $\zeta+\zeta^2+\zeta^3+\zeta^4+\zeta^5=-1,$ wenn man für $\zeta^3$ wieder $-1$ einsetzt.

Auflösen des Gleichungssystems ergibt $\zeta+\zeta^5=1$ und damit haben wir nur durch etwas Arithmetik mit den elementarsymmetrischen Ausdrücken der 6ten Einheitswurzeln eine Konstruktionsvorschrift für das Sechseck gewonnen, denn es gilt \[\cos(2\pi/6)=(\zeta+\zeta^5)/2=\frac{1}{2}\eqncomma\] wie man durch Betrachtung von kongruenten Dreiecken leicht sieht. Die $x$-Koordinate der 6ten Einheitswurzel $\zeta$ ist also $\frac{1}{2}.$ Zur Konstruktion des regelmäßigen Sechsecks muss man nur im Punkt $(\frac{1}{2},0)$ das Lot errichten, dessen Schnittpunkt mit dem Einheitskreis ist $\zeta.$

Für das Sechseck ist dies sicher kein sensationelles Resultat, aber es wird sich zeigen, dass Summen und Produkte von Einheitswurzeln bei der Konstruktion der anderen regelmäßigen Vielecke die entscheidende Rolle spielen werden.

Man kann sicher sein, dass Gauß, der ein leidenschaftlicher und virtuoser Rechner war, derartige Rechnungen mit Einheitswurzeln – und weit anspruchsvollere – auf Papier und im Kopf wiederholt durchgeführt hat und dass es diese Vertrautheit mit der Arithmetik der Einheitswurzeln war, die zu der plötzlichen Erkenntnis der Konstruierbarkeit des Siebzehnecks geführt hat.

Rückblick und Ausblick

Damit sind wir an einem Punkt angekommen, den der junge Gauß zu Anfang des Jahres 1796 ebenfalls erreicht hatte. Nur war der Weg für uns, die wir 200 zusätzliche Jahre der Mathematikgeschichte hinter uns haben, erheblich leichter. Komplexe Zahlen hatten damals noch keineswegs Bürgerrecht , Gauß selbst hat ihnen ja erst rund 30 Jahre später zum Durchbruch verholfen, und selbst die Eulersche Identität, die die Basis für Rechnungen mit Einheitswurzeln liefert, war damals erst 48 Jahre alt.

Im nächsten Abschnitt werden wir den eigentlichen Geniestreich des 19-jährigen präsentieren und es wäre heute noch ein Geniestreich, wenn ein Mathematikstudent des 21ten Jahrhunderts, der gegen Ende des zweiten oder dritten Semesters alles, was wir bisher zusammengetragen haben, aus dem Effeff  kennen sollte, von sich aus auf diese entscheidende Idee käme, die Gauß nach angestrengtem Nachdenken  morgens im Bette eingefahren ist.

Es bietet sich hier an, innezuhalten und zu rekapitulieren, welche Erkenntnisse wir bisher gewonnen haben: Wir wollen zeigen, dass bestimmte regelmäßige Vielecke mit Zirkel und Lineal konstruierbar sind. Wir haben die Eckpunkte eines regelmäßigen $n$-Ecks als komplexe $n$-te Einheitswurzeln identifiziert. Unsere Aufgabe besteht demnach im Nachweis, dass die Koordinaten bestimmter komplexer Einheitswurzeln in Form eines Ausdrucks dargestellt werden können, in dem nur Summen und Produkte von rationalen Zahlen und geschachtelte reelle Quadratwurzeln aus solchen Ausdrücken vorkommen.

Es genügt, diesen Nachweis für die $x$-Koordinate zu erbringen, denn alle Punkte mit dieser $x$-Koordinate liegen auf einer Parallelen zur $y$-Achse, die Einheitswurzeln liegen darüberhinaus auf dem Einheitskreis, so dass die $y$-Koordinate als Schnittpunkt von Kreis und Gerade ebenfalls konstruierbar ist.

Wenn man die $x$-Koordinate der Einheitswurzel $\zeta^1$ betrachtet, so ist diese nach Definition des regelmäßigen $n$-Ecks gleich $\cos(2\pi/n).$ Andererseits haben wir oben gesehen, dass die Summe einer Einheitswurzel mit ihrem konjugiert Komplexen eine reelle Zahl ergibt und speziell für $\zeta^1$ haben wir am Beispiel des Sechsecks gesehen: \[\zeta^1 + \bar{\zeta^1} = \zeta^1 + \zeta^{n-1} = 2\cos(2\pi/n)\eqndot\] Dass diese Beziehung für jedes regelmäßige $n$-Eck gilt, ergibt sich einfach aus der Definition der $n$-ten Einheitswurzel: \[\zeta^1 + \bar{\zeta^1} = \cos(2\pi/n)+\I\sin(2\pi/n)+\cos(2\pi/n)-\I\sin(2\pi/n)=2\cos(2\pi/n)\eqndot\]

Für das gleichseitige Dreieck sind wir damit übrigens schon fertig und können die Konstruktionsbeschreibung gleich hinschreiben, denn es gibt nur zwei dritte Einheitswurzeln ungleich $1$ und deren Summe ist einerseits $-1$ und andererseits $2\cos(2\pi/3)$. Wir haben also für die $x$-Koordinate von $\zeta_3$: $$ x = \cos(2\pi/3) = \frac{1}{2}(\zeta_3+\bar{\zeta_3})=\frac{1}{2}(\zeta_3+\zeta_3^2)=\frac{1}{2}(-1)=-\frac{1}{2}\eqndot $$ Das ist zwar nicht die übliche Konstruktionsweise für ein gleichseitiges Dreieck, aber es funktioniert.

Allgemein genügt es demnach, den gesuchten Quadratwurzelausdruck für $\zeta^1 + \zeta^{n-1},$ einer Summe von zwei Einheitswurzeln, zu finden. Dies, und die Tatsache, dass offenbar andere Summen und Produkte von Einheitswurzeln rationale, ja sogar ganze Zahlen sind, legt es nahe, sich mit Summen und Produkten von Einheitswurzeln zu befassen. Aber in welcher Art diese zu bilden sind, dazu bedurfte es sogar bei einem Gauß angestrengten Nachdenkens .