Konstruktionen mit Zirkel und Lineal

Schon in der Antike hat man sich mit geometrischen Konstruktionen beschäftigt, die nur mit Zirkel und Lineal auszuführen waren. Was dabei erlaubt und was verboten ist, hat Euklid in seinen Elementen  sehr rigide festgelegt:

Grundkonstruktionen

Zur Einübung soll hier kurz gezeigt werden, dass das Verbot, Längen zu übertragen, keine gravierende Einschränkung ist, denn eine Strecke lässt sich nur mit Hilfe erlaubter Konstruktionsschritte so parallel verschieben, dass ihr Anfangspunkt mit einem gegebenen Punkt zusammenfällt. Dazu zeigen wir zunächst, wie man von einem gegebenen Punkt das Lot auf eine Gerade fällt (siehe Abb.1).

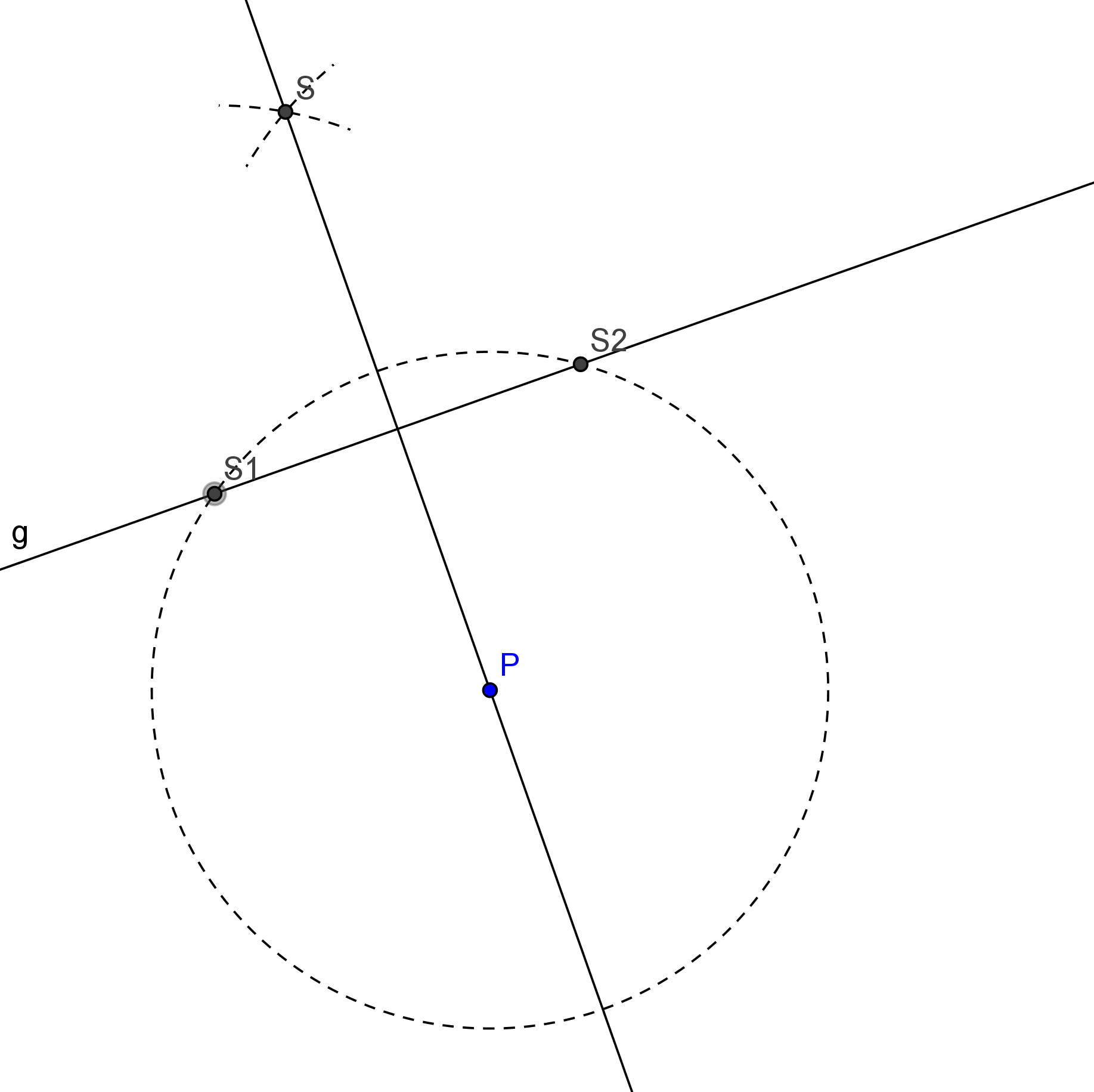
Gegeben sind der Punkt $P$ und die Gerade $g.$ Man zeichne um $P$ einen Kreis mit beliebigem Radius, der aber groß genug ist, dass der Kreis die Gerade $g$ schneidet. Die beiden Schnittpunkte sind $S1$ und $S2.$ Man zeichne den Kreis mit Mittelpunkt $S1$ durch $S2$ und den Kreis mit Mittelpunkt $S2$ durch $S1.$ Hier wird keine Länge übertragen, denn die Kreise haben zwar gleichen Radius, werden aber durch Mittelpunkt und Randpunkt eindeutig festgelegt. Die beiden Kreise schneiden sich in $S.$ Die Gerade $PS$ ist das Lot von $P$ auf $g.$ Diese Konstruktion funktioniert ebenfalls, wenn der Punkt $P$ auf der Geraden $g$ liegt, man spricht dann zwar meistens nicht davon, dass ein Lot gefällt  wird, sondern dass man die Senkrechte errichtet, die Konstruktion ist aber die gleiche und wir verwenden beide Sprechweisen, ohne hier einen Unterschied zu machen.

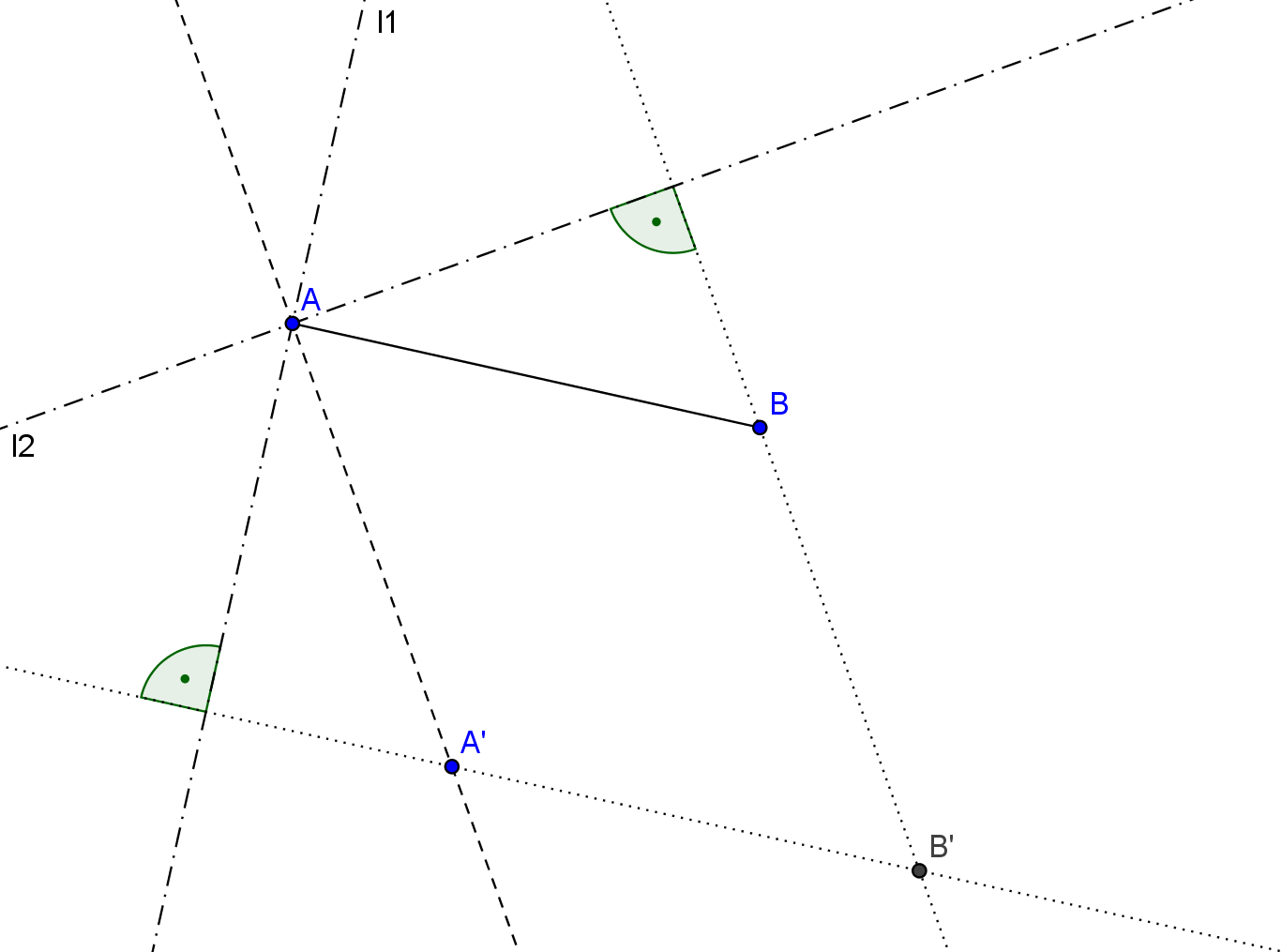
Soll nun die Strecke $AB$ parallel verschoben werden, so dass $A$ auf $A'$ zu liegen kommt (siehe Abb.2), so zeichnet man zunächst die Gerade durch $AA'.$ Dann errichtet man in $A$ sowohl das Lot $l1$ auf $AB$ wie auch das Lot $l2$ auf $AA'.$ Von $B$ fällt man das Lot auf $l2$ und von $A'$ das Lot auf $l1.$ Die Hilfskreise und -geraden zur Konstruktion der Senkrechten haben wir der Übersichtlichkeit halber weggelassen. Die beiden zuletzt errichteten Lote schneiden sich in $B'.$ $ABA'B'$ ist somit ein Parallelogramm, daher hat $A'B'$ die gleiche Länge und Richtung wie $AB.$

Bei derartigen Konstruktionen geht man immer von vorgegebenen  Punkten, Geraden oder Kreisen aus und erzeugt aus dieser Vorgabe mit Hilfe der erlaubten Konstruktionsschritte neue Punkte, Geraden und Kreise. Oft nimmt man als Standardvorgabe  für Konstruktionsaufgaben eine Strecke der Länge $1,$ oder was äquivalent ist, ein kartesisches Koordinatensystem, bei dem die Punkte $(0,0)$ und $(1,0)$ auf der $x$-Achse markiert sind. Bei der Konstruktion von regelmäßigen Vielecken gibt man meist ein kartesisches Koordinatensystem vor, in dem der Einheitskreis eingezeichnet ist, und verlangt, dass das Vieleck diesem Einheitskreis einbeschrieben wird, der Einheitskreis also Umkreis des Vielecks wird. Diese Vorgabe ist aber ebenfalls äquivalent zur Vorgabe einer Strecke der Länge $1.$

Im folgenden werden wir häufig über die Konstruierbarkeit von Punkten  in einem kartesischen Koordinatensystem sprechen. Ein solcher heißt mit Zirkel und Lineal konstruierbar, wenn seine $x$-Koordinate und seine $y$-Koordinate nach den Reglen des Euklid konstruierbar sind.

Addition und Subtraktion von Punktkoordinaten

Wir betrachten nur $x$-Koordinaten, weil das Verfahren für $y$-Koordinaten analog funktioniert. Ausgehend von zwei Punkten mit den Koordinaten $(a,0)$ und $(b,0)$ kann man den Punkt mit den Koordinaten $(a+b,0)$ leicht mit Hilfe der Parallelverschiebung konstruieren, indem man die Strecke mit den Endpunkten $(0,0)$ und $(b,0)$ entlang der $x$-Achse verschiebt, bis ihr Anfangspunkt mit dem Punkt $(a,0)$ zusammenfällt. Der Endpunkt der verschobenen Strecke ist dann der gesuchte Punkt mit den Koordinaten $(a+b,0)$. Das Vefahren funktioniert auch für negative Werte von $a$ oder $b$, wenn man darauf achtet, dass die Strecken ihre Orientierung, gegeben durch den Anfangspunkt $(0,0,)$ behalten. Der Punkt $(a-b,0)$ wird dann durch Addition des Punkts mit den Koordinaten $(-b,0)$ zu $(a,0)$ konstruiert. Ausgehend von einem Koordinatensystem mit den vorgegebenen Punkten $(0,0)$ und $(1,0)$ kann man demnach beliebige Punkte mit ganzzahligen  Koordinaten konstruieren.

Multiplikation und Division von Punktkoordinaten

Man kann mit Zirkel und Lineal auch multiplizieren und dividieren, wobei man den Strahlensatz anwendet. Zur Vereinfachung betrachten wir nur positive Werte, d.h. wir konstruieren zunächst Produkt bzw. Quotient der Beträge der Koordinaten und stellen das Vorzeichen anschließend richtig, indem wir das Ergebnis mit der richtigen Orientierung im Ursprung anheften. Darüberhinaus repräsentieren wir die zu multiplizierenden Punkte $(a,0)$ und $(b,0)$ durch Strecken der Länge $a$ bzw. $b$, die wir dorthin legen können, wo es uns passt.

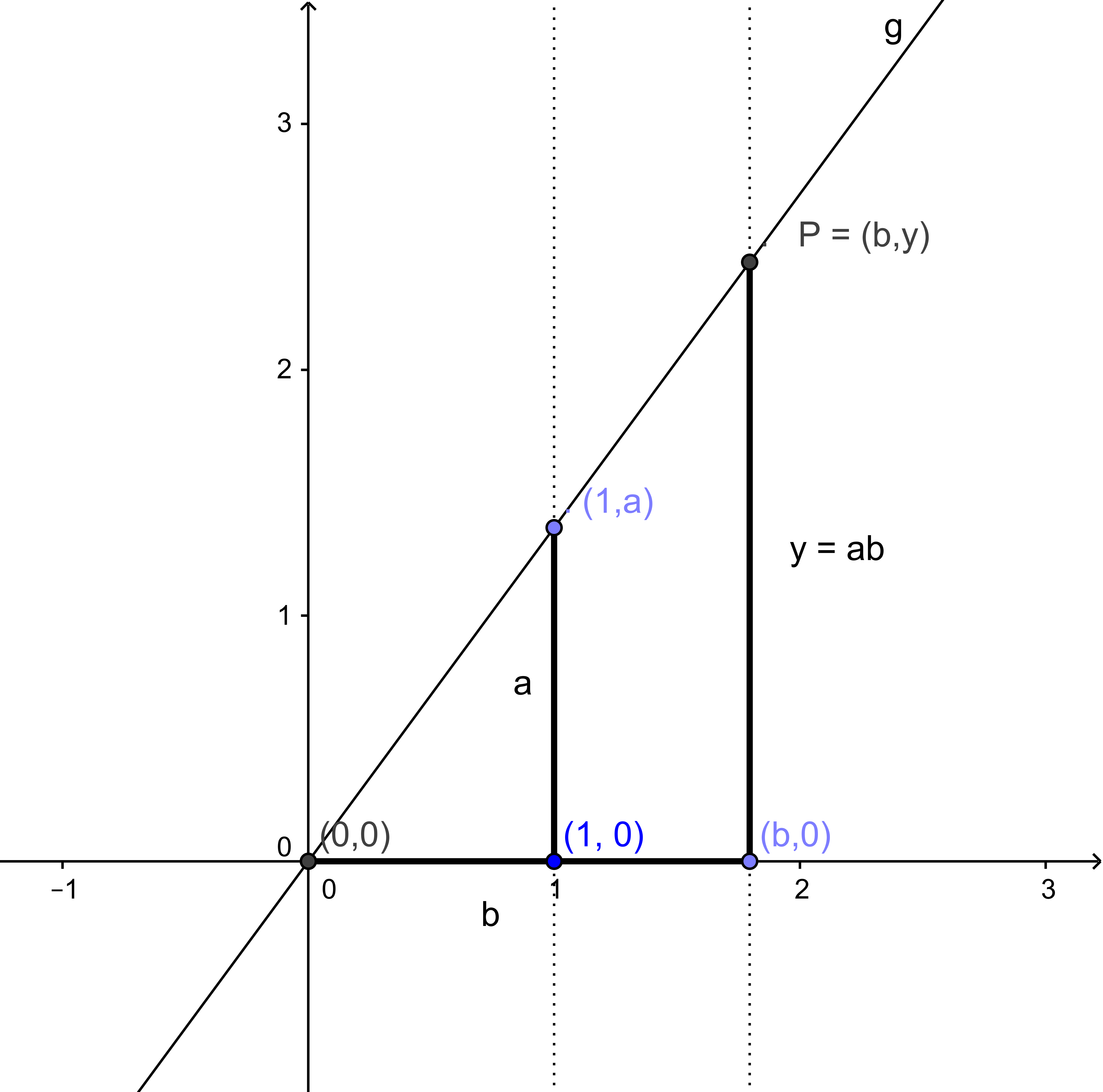
Es seien also die zwei Strecken der Länge $a$ bzw. $b$ gegeben. Man errichte im Punkt $(1,0)$ das Lot der Länge $a$ auf der $x$-Achse (siehe Abb.3). Sein Endpunkt ist demnach $(1,a).$ Man zeichne die Gerade $g$ durch den Ursprung $(0,0)$ und $(1,a).$ Dann errichte man das Lot im Punkt $(b,0)$ auf der $x$-Achse. Dieses Lot schneidet die Gerade $g$ in $P.$ Für die $y$-Koordinate von $P$ gilt nun nach dem Strahlensatz: \[\frac{a}{1} = \frac{y}{b}\:{\rm ,}\] also ist $y = ab$ und wir haben $a$ und $b$ multipliziert.

Zur Division führt man praktisch die gleiche Konstruktion durch, man muss nur $y$ als vorgegeben betrachten und $a$ als gesucht. Man errichtet also zunächst das Lot im Punkt $(b,0)$ der Länge $y,$ zeichnet die Gerade $g$ durch den Endpunkt $P = (b,y)$ und den Ursprung und errichtet im Punkt $(1,0)$ das Lot, das die Gerade $g$ in $(1,a)$ schneidet. Aus der obigen Gleichung $a = y/b$ folgt, dass man auf diese Weise $y$ durch $b$ dividiert hat.

Ausgehend von einem Koordinatensystem mit den vorgegebenen Punkten $(0,0)$ und $(1,0)$ kann man somit alle Punkte konstruieren, deren Koordinaten rationale  Zahlen, d.h. Brüche sind.

Lösen quadratischer Gleichungen

Etwas mehr Überlegung erfordert das Wurzelziehen mit Zirkel und Lineal, oder allgemeiner das Lösen einer quadratischen Gleichung $x^2 + ax + b = 0,$ wobei $a$ und $b$ rationale Zahlen sind (siehe dazu [Conway 1996]).

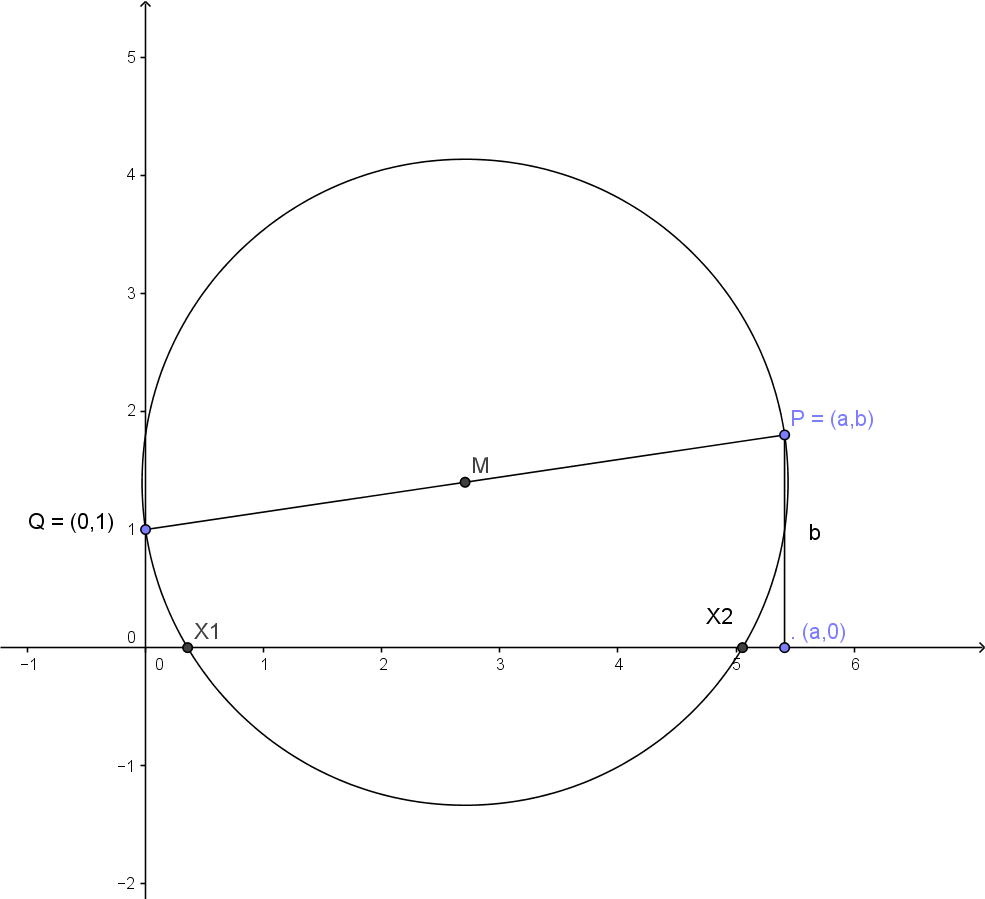
Wir betrachten dazu Abb.4 und konstruieren zunächst den Punkt $P = (a,b)$ mit rationalen Zahlen $a$ und $b.$ Die Menge der rationalen Zahlen wird üblicherweise mit $\mathbb{Q}$ bezeichnet, so dass wir dafür in Zukunft kurz $a,b \in \mathbb{Q}$ schreiben wollen.

Wir verbinden $P$ mit $Q = (0,1)$ und zeichnen den Kreis um den Mittelpunkt $M$ der Strecke $PQ$ durch $P$ bzw. $Q.$ Der Kreis schneidet die $x$-Achse (wenn wir Glück haben) in den Punkten $X1$ und $X2.$ Deren $x$-Koordinaten sind die Lösungen der Gleichung $x^2+ax+b=0.$

Zum Beweis stellt man zunächst fest, dass der Kreis nach Pythagoras den Durchmesser \[\sqrt{a^2 + (1-b)^2}\] hat. Der Mittelpunkt $M$ hat die $x$-Koordinate $a/2$ und die $y$-Koordinate $b + (1-b)/2 = (1+b)/2.$ Damit ergibt sich für die Kreislinie die Gleichung: \[(x-\frac{a}{2})^2 + (y-\frac{1+b}{2})^2 = \frac{a^2+(1-b)^2}{4} \:{\rm .}\] Für die Schnittpunkte des Kreises mit der $x$-Achse setzen wir $y=0$ und rechnen aus:

Die $x$-Koordinaten von $X1$ und $X2$ sind demnach tatsächlich die Lösung der vorgegebenen quadratischen Gleichung. Es ist eine gute Übung, sich davon zu überzeugen, dass dieser Ansatz auch für die extremen Fälle $a=0$ und $b=0$ funktioniert. Man sieht zudem, dass gewisse quadratische Gleichungen keine oder nur eine (reelle) Lösung haben, wenn der Kreis die $x$-Achse nicht schneidet oder nur in einem Punkt berührt. Dies ist z.B. speziell für $a=0$ und $b>0$ der Fall. Der Kreis kommt der $x$-Achse hier niemals näher als $\min(1,b),$ schneidet diese also nirgends. Die Lösungen von $x^2+b=0$ mit $b>0$ sind eben imaginär. Bei unseren Überlegungen zur Konstruierbarkeit müssen wir also darauf achten, dass die verwendeten quadratischen Gleichungen reelle Lösungen haben.

Insgesamt haben wir aber die Menge der konstruierbaren Punkte um diejenigen erweitert, deren Koordinaten reelle Lösungen von quadratischen Gleichungen mit rationalen Koeffizienten  sind. Dazu zählen natürlich speziell die Quadratwurzeln aus einer beliebigen nicht negativen rationalen Zahl $b$, die ja Lösungen von $x^2 - b = 0$ sind.

Die hier dargestellte Methode der Lösung einer quadratischen Gleichung mit Zirkel und Lineal soll übrigens auf den schottischen Schriftsteller Thomas Carlyle (1795-1881) zurückgehen, der, ehe er sich der Literatur zuwandte, einige Jahre als Mathematiklehrer gearbeitet hat. Die bei der Konstruktion beteiligten Kreise nennt man daher Carlyle-Kreise.

Aus den Regeln des Euklid ergibt sich, dass derart konstruierte Punkte wieder Ausgangspunkt für weitere Konstruktionsschritte sein können. $a$ und $b$ in der obigen Gleichung sind dann nicht rational sondern selbst von der Form $p \pm \sqrt{q}$ mit $p,q \in \mathbb{Q}$ und $q \geq 0.$ Die Lösung $x$ enthält somit zwei geschachtelte Quadratwurzeln. Man überlegt sich leicht, dass man mit den genannten Methoden jeden Punkt konstruieren kann, dessen Koordinaten durch einen endlichen Ausdruck gegeben sind, der neben rationalen Zahlen nur ineinander geschachtelte reellwertige Quadratwurzeln enthält, die durch die vier Grundrechenarten verknüpft sind. Um die Konstruktion wirklich durchzuführen, werden die Wurzeln von Innen nach Außen abgearbeitet. Wenn etwa eine Koordinate durch \[ x = \sqrt{a + \sqrt{b + \sqrt{c}}} \] gegeben ist, mit $a,b,c \in \mathbb{Q},$ konstruiert man zunächst mit Hilfe des Strahlensatzes $c, b$ und $a$ als rationale Zahlen. Dann folgt $\sqrt{c}$ als Lösung der quadratischen Gleichung $x_1^2 - c = 0$ wie oben beschrieben. Man bildet $x_2 = x_1 + b$ durch Addition und löst $x_3^2 - x_2 = 0$ wieder wie oben usw., wobei wir voraussetzen, dass die Ausdrücke unter dem Wurzelzeichen immer nicht negativ sind.

Man ist also wirklich berechtigt, eine solche Kette ineinandergeschachtelter und miteinander verknüpfter Quadratwurzeln als Konstruktionsbeschreibung  für eine Euklidische Konstruktion mit Zirkel und Lineal aufzufassen. In genau dieser Form hat Gauß die Konstruktionsbeschreibung des Siebzehnecks angegeben und in genau dieser Form erzeugt das weiter unten beschriebene Java-Programm die Konstruktionsbeschreibung für die regelmäßigen Vielecke mit primer Eckenzahl.

Im Allgemeinen, auch bei den regelmäßigen Vielecken, ist eine solche Konstruktion, die direkt aus dem Wurzelausdruck abgeleitet wird, natürlich nicht sonderlich elegant – um es vorsichtig auszudrücken. Man könnte sie eher als überwältigend umständlich bezeichnen. Aber darum soll es uns nicht gehen. Für den Nachweis der Konstruierbarkeit reicht es, irgendeine  Konstruktionsbeschreibung anzugeben, die Vereinfachung und Verschönerung ist sicher eine reizvolle Aufgabe, bringt aber keinen Erkenntnisgewinn.

Die folgende rekursive Definition dessen, was man unter einem konstruierbaren Punkt  versteht, kann man daher als Zusammenfassung dessen verstehen, was eine Konstruktionsbeschreibung in unserem Sinne ausmacht:

Ohne das ganze Arsenal der Algebra hier aufzufahren, sei daran erinnert, dass man eine Struktur, in der die vier Grundrechenarten unbeschränkt ^[1] ausgeführt werden können, als Körper  bezeichnet. Die rationalen Zahlen $\mathbb{Q}$ bilden einen Körper, ebenso wie die reellen Zahlen $\mathbb{R}$ oder die komplexen Zahlen $\mathbb{C}.$ In dem obigen Kasten wird recht umständlich beschrieben, dass man aus $\mathbb{Q}$ neue Körper, sogenannte Erweiterungskörper , erzeugen kann, wenn man einzelne Wurzeln hinzunimmt und mit diesen wie üblich rechnet.

Als bequeme, wenn auch etwas schludrige Sprechweise, werden wir das Ergebnis des im obigen Kasten beschriebenen Verfahrens manchmal einfach nur als Quadratwurzelausdruck  oder gar als Wurzelausdruck  bezeichnen.

Wir haben bisher gezeigt, dass jeder Wurzelausdruck mit Zirkel und Lineal abgearbeitet und geometrisch realisiert werden kann. Wir wollen jedoch noch die Umkehrung  beweisen, dass jeder geometrisch nach Euklid konstruierte Punkt Koordinaten hat, die durch einen derartigen Wurzelausdruck gegeben sind – deswegen haben wir bei der obigen Zusammenfassung von einer vorläufigen Fassung gesprochen.

Schnittpunkte von Geraden

Dazu reicht es zu zeigen, dass die Koordinaten der Schnittpunkte von Geraden, von Geraden mit Kreisen oder von zwei Kreisen immer als Wurzelausdrücke der obigen Form darstellbar sind.

Die $x$-Koordinate des Schnittpunkts zweier Geraden $y = m_1x + c_1$ und $y = m_2x + c_2$ ergibt sich durch Gleichsetzen:

\[ m_1x + c_1 = m_2x + c_2 \] \[ x = \frac{c_2-c_1}{m_1-m_2}\:{\rm .} \] Wenn beispielsweise die erste Gerade durch zwei Punkte \[ (x_1,y_1) = (p_1+\sqrt{q_1},v_1 + \sqrt{w_1}) \] und \[ (x_2,y_2) = (p_2+\sqrt{q_2},v_2 + \sqrt{w_2}) \] gegeben ist (wir beschränken uns auf positive Wurzelvorzeichen), hat man für $m_1$ und $c_1$ \[m_1 = \frac{y_1-y_2}{x_1-x_2}\] und \[c_1 = \frac{y_1(x_1-x_2)-x_1(y_1-y_2)}{x_1-x_2}\:{\rm .}\] Eingesetzt ergibt sich \[m_1 = \frac{v_1 + \sqrt{w_1}-v_2 - \sqrt{w_2}}{p_1+\sqrt{q_1}-p_2-\sqrt{q_2}}\] und \[c_1 = \frac{(v_1 + \sqrt{w_1})(p_1+\sqrt{q_1}-p_2-\sqrt{q_2})-(p_1+\sqrt{q_1})(v_1 + \sqrt{w_1}-v_2 - \sqrt{w_2})}{p_1+\sqrt{q_1}-p_2-\sqrt{q_2}}\:{\rm .}\] Analoge Ausdrücke ergeben sich für $m_2$ und $c_2.$ Eingesetzt in die Gleichung der $x$-Koordinate des Schnittpunkts bekommt man einen Ausdruck der gewünschten Art. Gleiches gilt für die $y$-Koordinate.

Der Grund dafür ist natürlich, dass die Gleichungen für $x$, $m_1$ und $c_1$ rationale Funktionen der $x_1, x_2, y_1, y_2$ sind, wobei Zähler und Nenner jeweils aus Polynomen ersten Grades bestehen (keine Quadrate, Kuben etc.). Wenn man in so eine Funktion einen gültigen Wurzelausdruck einsetzt, bekiommt man nach Definition wieder einen gültigen Wurzelausdruck.

Schnittpunkte von Kreisen

Wir zeigen hier noch, dass die Koordinaten der Schnittpunkte zweier Kreise Lösung einer quadratischen Gleichung sind und überlassen die Untersuchung des Falls Gerade schneidet Kreis  dem Leser.

Zunächst stellen wir fest, dass der Abstand zweier Punkte $(x_1,y_1)$ und $(x_2,y_2)$ durch \[ r = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \] gegeben ist. Setzt man hier für die Koordinaten die obigen Wurzelausdrücke ein, erhält man wiederum nur geschachtelte Quadratwurzeln, die durch die vier Grundrechenarten miteinander verknüpft sind. Wir dürfen also die Kreisgleichung für einen Kreis mit Mittelpunkt $(x_1,y_1)$ in der Form \[ (y-y_1)^2 + (x-x_1)^2 = r_1^2 \] schreiben, mit dem Radius $r_1,$ der durch einen geschachtelten Quadratwurzelausdruck dargestellt werden kann.

Den Schnittpunkt zweier Kreise berechnen wir, indem wir zwei Kreisgleichungen dieser Art als Gleichungssystem auffassen und subtrahieren: \[(y-y_1)^2 + (x-x_1)^2 = r_1^2 \] \[(y-y_2)^2 + (x-x_2)^2 = r_2^2 \] Ergibt nach Subtraktion: \[-2yy_1 + y_1^2 +2yy_2 - y_2^2 -2xx_1 + x_1^2 + 2xx_2 - x_2^2 = r_1^2-r_2^2 \:{\rm .}\] Entscheidend ist, dass $x^2$ und $y^2$ dabei wegfallen, man erhält also z. B. für $y$ einen Ausdruck, der linear in $x$ ist (nämlich die Geradengleichung der sog. Chordale  der beiden Kreise):

Durch Einsetzen dieses Wertes in eine der beiden Kreisgleichungen erhält man zwar einen ziemlich unübersichtlichen Ausdruck, von dem man aber weiß, dass er eine quadratische Gleichung für $x$ ist. Als Lösung einer quadratischen Gleichung ist die $x$-Koordinate des Schnittpunkts zweier Kreise ein Ausdruck, in dem neben den elementaren Rechenoperationen nur Quadratwurzeln aus den $x_1,x_2,y_1,y_2 , r_1,r_2$ vorkommen. Das gleiche gilt für die $y$-Koordinate.

Hauptsatz zur Konstruierbarkeit

Wenn man in den so erhaltenen Ausdrücken für $x$ und $y$ die $x_1,\dots,r_2$ selbst wieder durch Wurzelausdrücke ersetzt, es handelte sich ja um konstruierbare Kreise, bei denen das nach Voraussetzung möglich ist, erhält man insgesamt einen Ausdruck, in dem neben den elementaren Operationen Addition, Subtraktion, Multiplikation und Division nur rationale Zahlen und geschachtelte Quadratwurzeln vorkommen. Wir halten fest: Die nach Euklid erlaubten Konstruktionsschritte führen immer zu Punkten, deren Koordinaten durch Ausdrücke der oben beschriebenen Art gegeben sind. Die dort gemachte Aussage kann demnach wie folgt verschärft werden: