Die komplexe Zahlenebene

Im ersten Kapitel haben wir unsere Konstruktionen in einem kartesischen Koordinatensystem durchgeführt, in dem die Koordinaten als reelle Zahlen gegeben waren, die konstruierbaren Koordinaten waren sogar nur eine Untermenge der reellen Zahlen, eben die mehrfach zitierten Wurzelausdrücke.

Es stellt sich jedoch heraus, dass viele Konstruktionsaufgaben, insbesondere die Kreisteilung, viel eleganter gelöst werden können, wenn man die komplexe Zahlenebene  zugrunde legt.

Nun scheint es von Bundesland zu Bundesland unterschiedlich zu sein, ob komplexe Zahlen in der gymnasialen Oberstufe behandelt werden oder nicht (z.T. abhängig vom G8 oder G9). Ich kann also wohl nicht voraussetzen, dass jeder schon einmal mit dem Körper $\mathbb{C}$ der komplexen Zahlen in Berührung gekommen ist. Deshalb folgt hier ein Crashkurs  zu diesem Thema, wobei wir uns auf die Fakten beschränken, die in den folgenden Kapiteln gebraucht werden. Alternativ (und besser) kann man sich auf vielen Seiten im Web über die Grundlagen informieren, wenn man nach komplexe Zahlen Schulstoff  googelt.

In meiner Schulzeit (Mitte der 60er Jahre) wurden in der Oberstufe zunächst die imaginären  Zahlen mit der Motivation eingeführt, dass man für die Gleichung $x^2+1=0$ eine Lösung haben möchte. Dazu wird der Zahlbereich der reellen Zahlen $\mathbb{R}$ erweitert, indem man die positive Quadratwurzel aus $-1$ hinzunimmt. Man setzt \[ \I = \sqrt{-1} \] und hat damit Lösungen der obigen Gleichung gefunden, nämlich $\pm\I.$

Wenn man in diesem so erweiterten Zahlbereich wie üblich addieren und multiplizieren will, kommt man zwangsläufig zu Ausdrücken der Form $a + b\I$ mit $a, b \in \mathbb{R}$ und bezeichnet diese Ausdrücke als komplexe Zahlen 

Die Regeln für Addition, Subtraktion und Multiplikation dieser komplexen Zahlen ergeben sich ebenfalls zwangsläufig: $$ (a + b\I) + (c + d\I) = (a+c)+(b+d)\I $$ $$ (a + b\I) - (c + d\I) = (a-c)+(b-d)\I $$ und $$ (a + b\I)(c + d\I)=ac + bc\I + ad\I + bd\I^2=(ac-bd) + (bc+ad)\I $$ wobei $\I^2 = -1$ berücksichtigt wurde.

Etwas trickreicher ist die Regel für die Division abzuleiten, die selbstverständlich nur für Divisoren ungleich $0$ erlaubt ist: $$ \frac{a + b\I}{c + d\I} = \frac{(a + b\I)(c - d\I)}{(c + d\I)(c - d\I)} = \frac{(ac+bd) + (bc-ad)\I}{c^2+d^2} = \frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2}\I $$ Man erweitert den Bruch, damit die komplexe Zahl im Nenner wegfällt und man die normale Darstellung erhält.

Man verifiziert leicht, dass für das Rechnen mit komplexen Zahlen die gleichen Gesetze (Kommutativgesetz, Assoziativgesetz, Distributivgesetz, Existenz von neutralen Elementen und Inversen) gelten wie für die reellen Zahlen, dass die komplexen Zahlen also einen Körper  bilden, den man mit $\mathbb{C}$ bezeichnet und der die reellen Zahlen $\mathbb{R}$ als Unterkörper enthält, die reellen Zahlen können nämlich als spezielle komplexe Zahlen der Form $a+0\I$ aufgefasst werden.

Für unsere Betrachtungen zur Konstruierbarkeit ist jedoch ein anderer Aspekt der komplexen Zahlen noch wichtiger, nämlich dass mit ihrer Hilfe die Drehung eines Punktes in der Ebene um den Ursprung $(0,0)$ eine einfache arithmetische Entsprechung bekommt, in Form der Multiplikation von komplexen Zahlen.

Geometrische Interpretation der komplexen Zahlen

Wurzeln aus negativen Zahlen, die erstmals im Zusammenhang mit der Lösung der kubischen Gleichung als nützliche Hilfskonstruktionen erkannt worden waren, führten bis Ende des 18ten Jahrhunderts eine spukhafte Existenz, worauf schon die Bezeichnung imaginäre  Zahlen hindeutet. Erst mit der geometrischen Interpretation der komplexen Zahlen, die unabhängig voneinander durch den Norweger Caspar Wessel (1745-1818) um 1799, den Franzosen Jean Robert Argand (1768-1822) um 1806 und schließlich durch Gauß um 1831 vorgestellt wurde, fanden die komplexen Zahlen allgemeine Anerkennung.

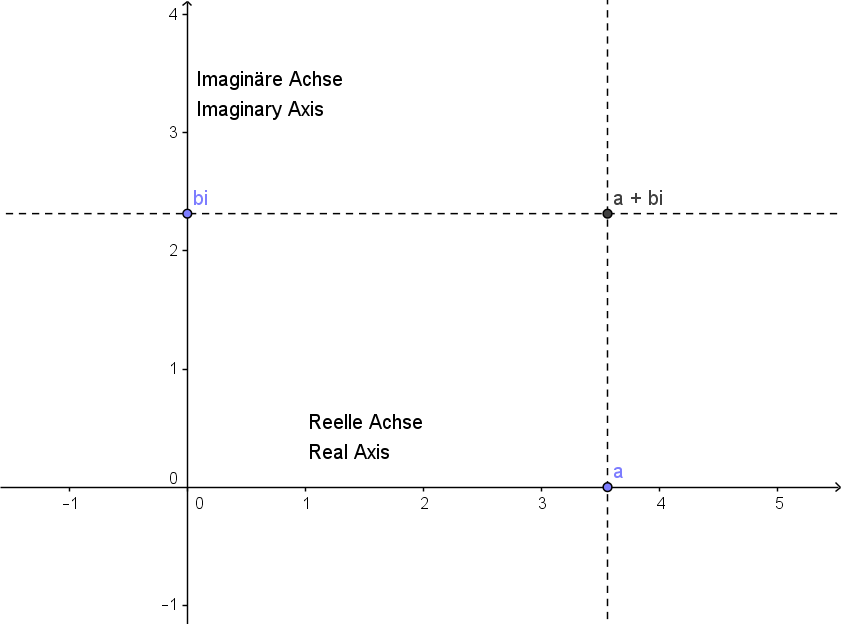
Eine komplexe Zahl $a + b\I$ wird dabei als Punkt in der Ebene mit den Koordinaten $(a,b)$ interpretiert (siehe Abb.1). Auf der horizontalen Achse liegen demzufolge die reellen Zahlen $a = a+0\I,$ auf der vertikalen Achse die rein imaginären Zahlen $b\I = 0 + b\I.$ Die so interpretierte Ebene nennt man komplexe Zahlenebene  oder Gaußsche Zahlenebene  oder auch Argandsche Zahlenebene  – Wessels Beitrag, der erst hundert Jahre nach seiner Veröffentlichung in den Abhandlungen der Königlich Dänischen Akademie der Wissenschaften entdeckt wurde, hat die verdiente Würdigung leider nicht erfahren.

Addition von komplexen Zahlen

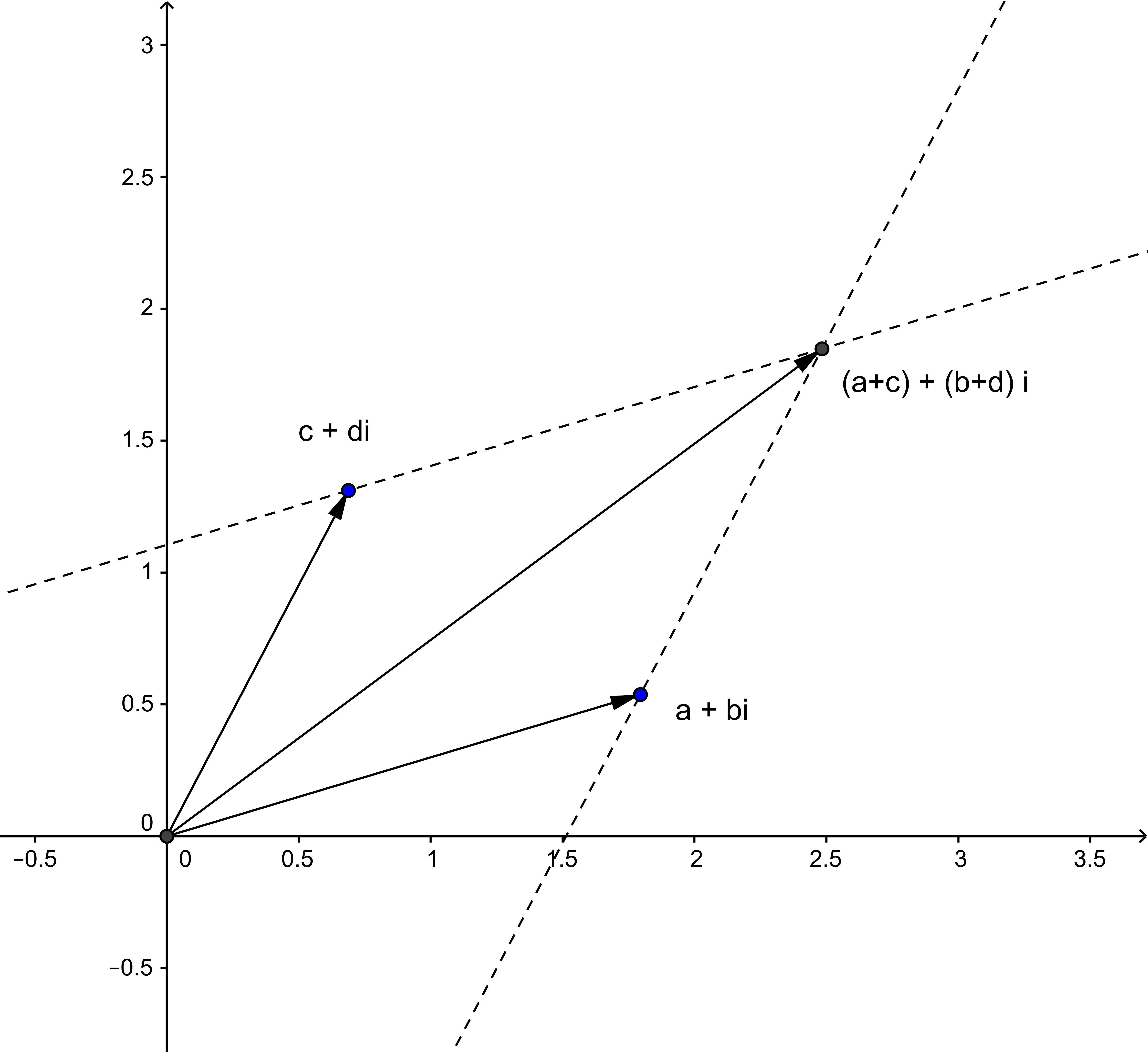
Für die Veranschaulichung der arithmetischen Operationen in der komplexen Zahlenebene ist es nützlich, sich die komplexen Zahlen nicht als Punkte  in der Zahlenebene vorzustellen sondern als Vektoren , die vom Ursprung zu dem entsprechenden Punkt zeigen.

Die Addition zweier komplexer Zahlen $a+b\I$ und $c+d\I$ erfolgt durch getrennte Addition von Realteil und Imaginärteil: \[ (a + b\I) + (c + d\I) = (a+c) + (b+d)\I\eqndot \] Dies entspricht der üblichen Addition von Vektoren (siehe Abb.2), wie man sie vom Kräfteparallelogramm in der Physik kennt und ist eine direkte Verallgemeinerung der Addition von reellen Zahlen auf dem Zahlenstrahl . Man sieht sofort, dass die Addition komplexer Zahlen eine mit Zirkel und Lineal lösbare Konstruktionsaufgabe ist.

Polarkoordinaten

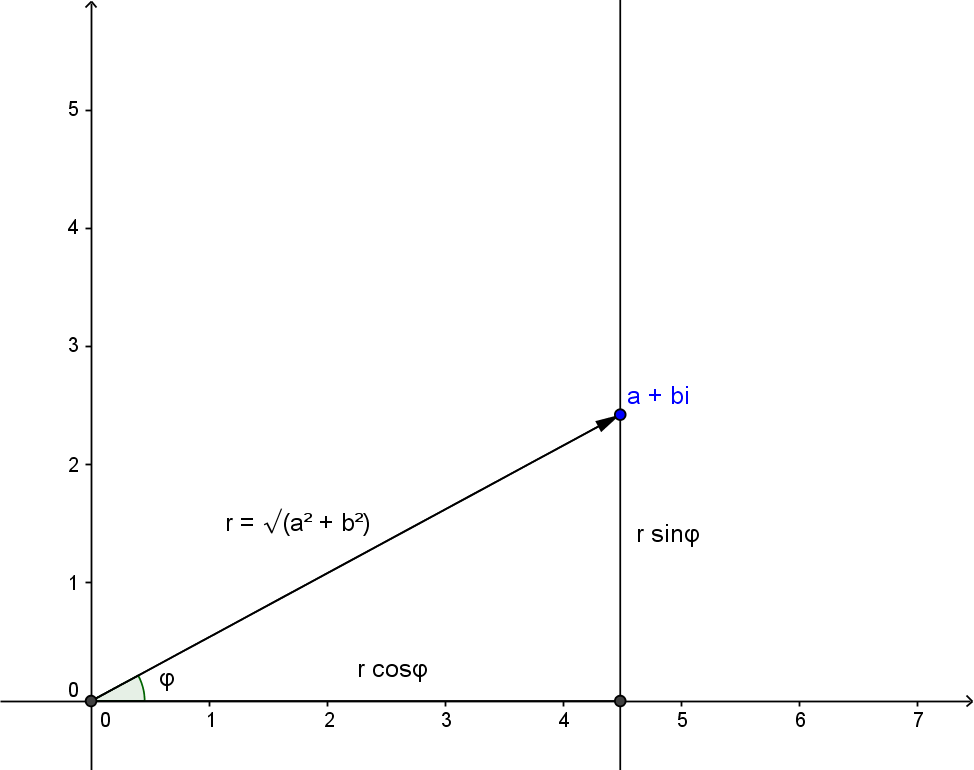
Für die Multiplikation greift man auf eine dritte Darstellungsform der komplexen Zahlen zurück. Der Vektor, der vom Ursprung zur komplexen Zahl $a+b\I$ führt, ist nämlich Hypotenuse in einem rechtwinkligen Dreieck, mit den Katheten der Längen $a$ und $b.$ Nach Pythagoras hat diese Hypotenuse die Länge \[r = \sqrt{a^2 + b^2}\eqndot \] Wenn $\varphi$ den Winkel des Vektors mit der reellen Achse bezeichnet (siehe Abb.3), gilt \[a = r \cdot \cos \varphi\] und \[b = r \cdot \sin \varphi\eqndot\] Die komplexe Zahl $a+b\I$ ist also eindeutig durch das Paar $(r,\varphi)$ mit $0 \leq \varphi \lt 360^{\circ}$ gegeben. Diese Art von Koordinaten, gegeben durch Abstand vom Ursprung und Winkel des Vektors mit der reellen Achse, bezeichnet man als Polarkoordinaten . Den Winkel $\varphi$ bezeichnet man in diesem Zusammenhang auch als Polarwinkel  oder Argument.

Der Abstand vom Ursprung heißt Betrag  der komplexen Zahl \[r = \sqrt{a^2+b^2} =: |a+b\I|\eqndot\] Man sieht sofort, dass \[ |a+b\I|^2 = a^2 + b^2 = (a+b\I)(a-b\I)\] gilt. Für die komplexe Zahl $z = a+b\I$ bezeichnet man die an der reellen Achse gespiegelte komplexe Zahl $\bar{z} = a-b\I$ als die zu $z$ konjugierte  komplexe Zahl und hat für den Betrag von $z$: \[ |z| = \sqrt{z\bar{z}}\eqndot\]

Es ist eine gute Übung, in diesem Zusammenhang nachzuweisen, dass das Konjugierte einer Summe $\overline{z_1+z_2}$ gleich der Summe der Konjugierten $\bar{z_1}+\bar{z_2}$ ist und dass das Konjugierte des Produkts $\overline{z_1z_2}$ gleich dem Produkt der Konjugierten $\bar{z_1}\cdot\bar{z_2}$ ist. Außerdem wird hier klar, wie man auf den oben benutzten Trick bei der Division von komplexen Zahlen gekommen ist.

Statt das Paar $(r,\varphi)$ anzugeben, schreibt man häufig \[a + b\I = r(\cos\varphi + \I\sin\varphi)\] oder unter Verwendung der berühmten Identität von Leonhard Euler (1707-1783) \[e^{\I\varphi} = \cos\varphi + \I\sin\varphi\] auch \[a + b\I = re^{\I\varphi}\eqndot\] Die Eulersche Identität ergibt sich aus der Reihendarstellung der Exponentialfunktion, die glücklicherweise immer noch zum Schulstoff gehört: $$ e^x = \sum_{n=0}^\infty \frac{x^n}{n!} $$ Setzt man hier für $x$ den Wert $\I\varphi$ ein, erhält man: $$ e^{\I\varphi} = \sum_{n=0}^\infty \frac{\I^n\varphi^n}{n!} = 1 + \I\varphi + \frac{\I^2\varphi^2}{2!} + \frac{\I^3\varphi^3}{3!} + \frac{\I^4\varphi^4}{4!} + \dots $$ Nun ist $\I^0=1, \I^1=\I, \I^2=-1, \I^3=-\I, \I^4=+1, \I^5=+\I,\dots$ und man sieht, dass die Reihe in zwei Teile für gerade  und ungerade  $n$ zerfällt: $$ e^{\I\varphi} = (1 - \frac{\varphi^2}{2!} + \frac{\varphi^4}{4!} - \dots) + \I\,(\varphi - \frac{\varphi^3}{3!} + \frac{\varphi^5}{5!} - \dots)=: c(\varphi)+\I\, s(\varphi) $$ Dass die Ausdrücke in den Klammern $c(\varphi)$ und $s(\varphi)$ genau die Reihenentwicklungen für $\cos\varphi$ bzw. $\sin\varphi$ sind, scheint nun dummerweise nicht mehr zum Schulstoff zu gehören. Wer diese Darstellung noch nie gesehen hat, muss mir leider einfach glauben oder möge durch gliedweises Differenzieren der Reihen nachrechnen, dass die Funktionen $c(\varphi)$ und $s(\varphi)$ die Differentialgleichungen $s'(\varphi) = c(\varphi)$ und $c'(\varphi)=-s(\varphi)$ erfüllen – genau wie $\sin\varphi$ und $\cos\varphi.$ Dann muss er mir nur noch zu glauben, dass dadurch – und durch die Randbedingungenm $c(0)=1$ bzw. $s(0)=0$ die trigonometrischen Funktionen $\cos$ und $\sin$ eindeutig bestimmt sind.

Multiplikation von komplexen Zahlen

Die Darstellung mit Polarkoordinaten erlaubt nun eine besonders einfache geometrische Interpretation der Multiplikation von komplexen Zahlen. Wie oben gesehen gilt für die Multiplikation: \[(a+b\I)(c+d\I) = (ac - bd) + (ad+bc)\I\eqndot\] Verwendet man Polarkoordinaten \[a + b\I = u(\cos\alpha + \I\sin\alpha)\] und \[c + d\I = v(\cos\beta + \I\sin\beta)\eqncomma\] ergibt sich \[(a+b\I)(c+d\I) = uv(\cos\alpha\cos\beta - \sin\alpha\sin\beta) + uv(\cos\alpha\sin\beta + \sin\alpha\cos\beta)\I\eqndot\] Dies ist aber nach dem aus der Schule bekannten Additionstheorem für Winkelfunktionen nichts anderes als: \[(a+b\I)(c+d\I) = uv(\cos(\alpha+\beta) + \I\sin(\alpha+\beta))\eqndot\] Bei der Multiplikation von komplexen Zahlen, die in Polarkoordinaten gegeben sind, werden die Beträge der Zahlen multipliziert und die Argumente (Polarwinkel) addiert. Die Multiplikation ist demnach geometrisch eine Drehstreckung .

Die Darstellung als Exponentialfunktion lässt diesen Zusammenhang besonders deutlich werden: \[ue^{\I\alpha}\cdot ve^{\I\beta} = uve^{\I(\alpha+\beta)}\eqncomma\] einfach aufgrund der Multiplikationsregeln für Potenzen.

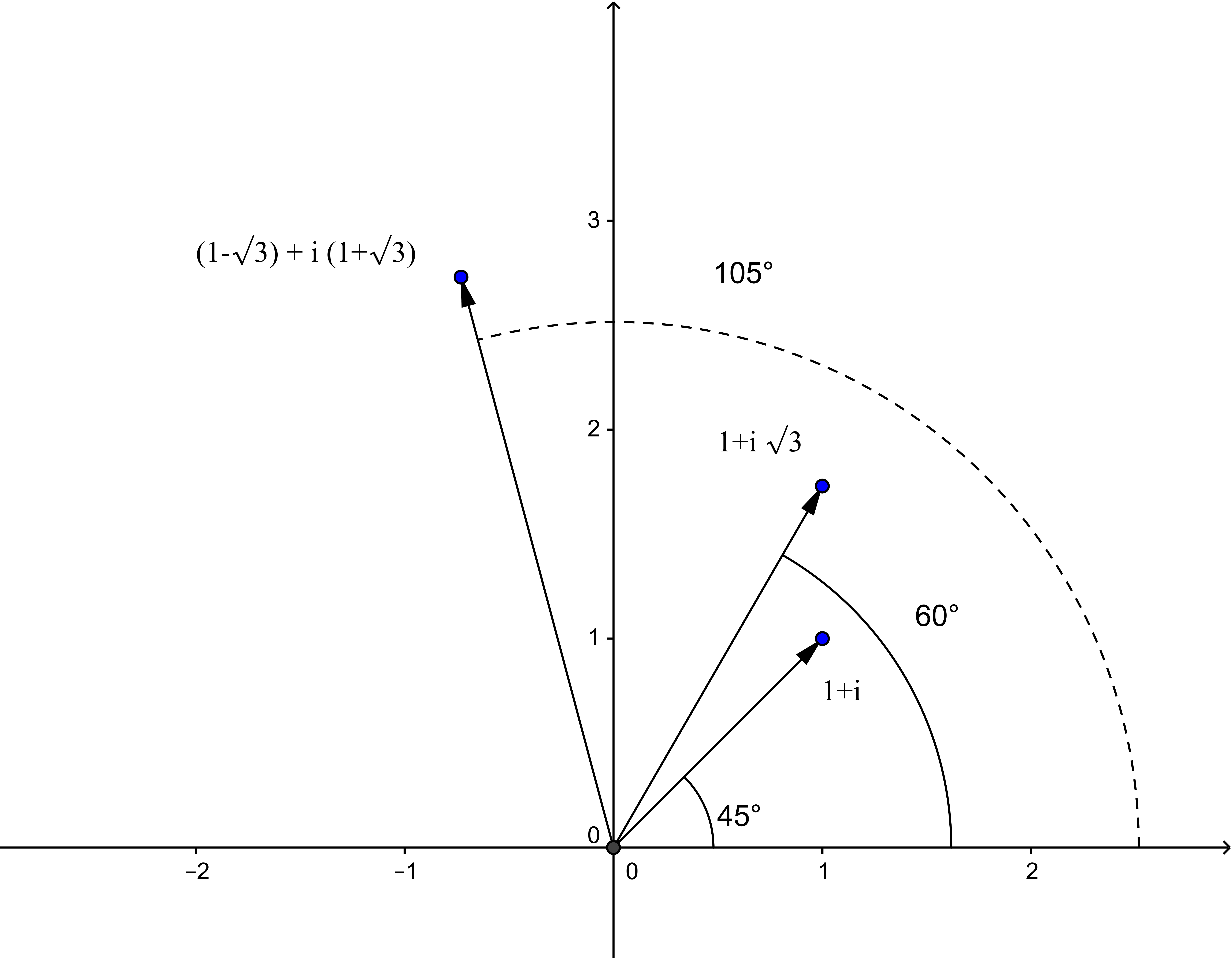
Zur Veranschaulichung betrachte man das Beispiel in Abb.4. Führt man die Multiplikation arithmetisch aus, ergibt sich: \[(1+\I)(1+\I\sqrt{3}) = (1-\sqrt{3}) + \I(1+\sqrt{3})\eqndot\] In Polarkoordinaten: \[1+\I = \sqrt{2}(\cos(45^{\circ})+\I\sin(45^{\circ}))\] \[1+\I\sqrt{3} = \sqrt{4}(\cos\alpha + \I\sin\alpha)\] Für $\alpha$ gilt $\tan\alpha = \sqrt{3},$ also $\alpha = 60^{\circ}.$ Multiplikation der Beträge ergibt: \[|1+\I|\cdot|1+\I\sqrt{3}| = \sqrt{2}\sqrt{4} = 2\sqrt{2}\] und andererseits ist der Betrag des Produkts: \[|(1-\sqrt{3}) + \I(1+\sqrt{3})| = \sqrt{4-2\sqrt{3}+4+2\sqrt{3}} = \sqrt{8} = 2\sqrt{2}\eqndot\] Für den Polarwinkel $\varphi$ des Produktvektors gilt: \[\tan \varphi = \frac{1+\sqrt{3}}{1-\sqrt{3}} = -(2+\sqrt{3})\eqncomma\] wie man leicht sieht, wenn man den Bruch mit $1+\sqrt{3}$ erweitert und ausmultipliziert. In den Tabellen für die Winkelfunktionen findet man zu diesem Wert von $\tan\varphi$ den Winkel $\varphi = 105^{\circ},$ die Summe der Polarwinkel der multiplizierten Zahlen.

Mehr muss man gar nicht von den komplexen Zahlen oder der Gaußschen Zahlenebene wissen, um die folgenden Kapitel zu verstehen. Wir werden uns in diesen fast ausschließlich mit ganz speziellen komplexen Zahlen befassen, den komplexen Wurzeln aus Eins, auch Einheitswurzeln  genannt. Wer sich intensiver mit komplexen Zahlen und ihrer kaum zu überschätzenden Bedeutung für Mathematik und Physik beschäftigen will, sei auf die beiden Bücher von Paul J. Nahin [Nahin 1998] und [Nahin 2006] verwiesen.