Constructions with Ruler and Compass
Already in ancient Greece mathematicians thought about geometric constructions to be performed by ruler (or straightedge) and compass. Euclid in his Elements gave a set of rigorous rules of what is permitted and what is not, when performing such a construction:
- The ruler may only be used to draw a line segment between two points that have been already constructed or to extend such a line segment to arbitrary length. Markers on the ruler, by which distances can be measured or by which lines are fitted into place are not permitted.
- The compass may be used to draw a circle of arbitrary radius around a point that has already been constructed (the center). The arbitrariness of the radius of course includes the possibility to draw a circle through a given point other than the center. The compass is assumed to collapse as soon as it is lifted from the page so that the radius is no more available. Hence the compass may not be used to transfere distances.
- The points of intersection of lines and circles drawn in this way are regarded as constructed points.
Basic Constructions
To become familiar with these rules it shall be shown that it is no severe restriction, to refrain from transferring distances with the compass. You will see that it is possible, using only legal operations, to perform a parallel translation of a given line segment so that one of its points coincides with a given point. To do so, we have to show beforehand, how to construct the perpendicular to a line through a given point (see fig.1).
[Show in new tab]
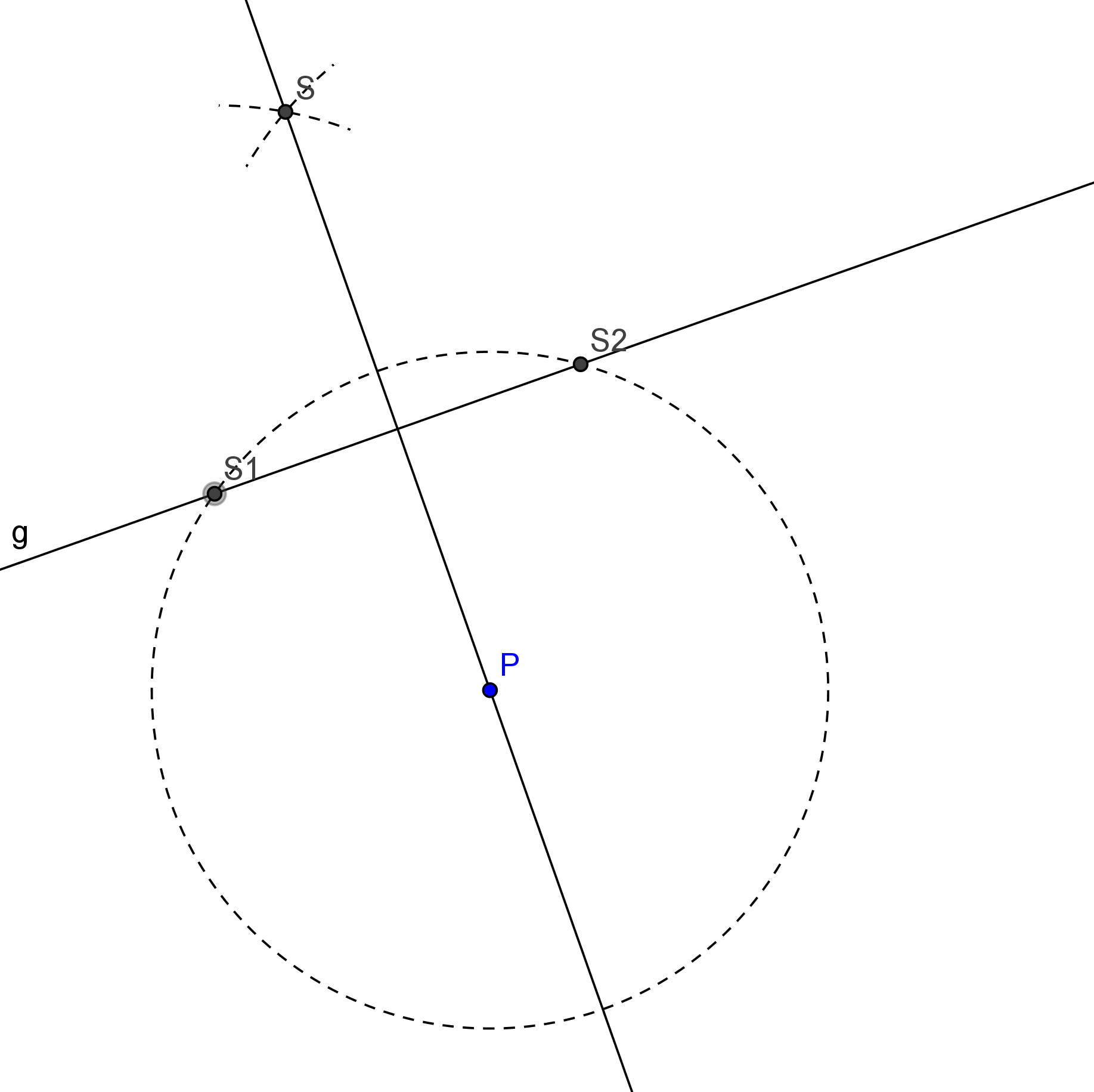
Given the point $P$ and the line $g$ you draw a circle around $P$ with arbitrary radius, but large enough to intersect with $g$. The two points of intersection are $S1$ and $S2.$ Now you draw a circle with center $S1$ through $S2$ and a circle with center $S2$ through $S1.$ This is no illegal transfer of a distance, although the radius of the circles is the same, because both circles are constructed independently. The two circles intersect in $S.$ The line segment $PS$ is the perpendicular through $P$ to $g.$ This construction works, even if the point $P$ lies on the line $g.$
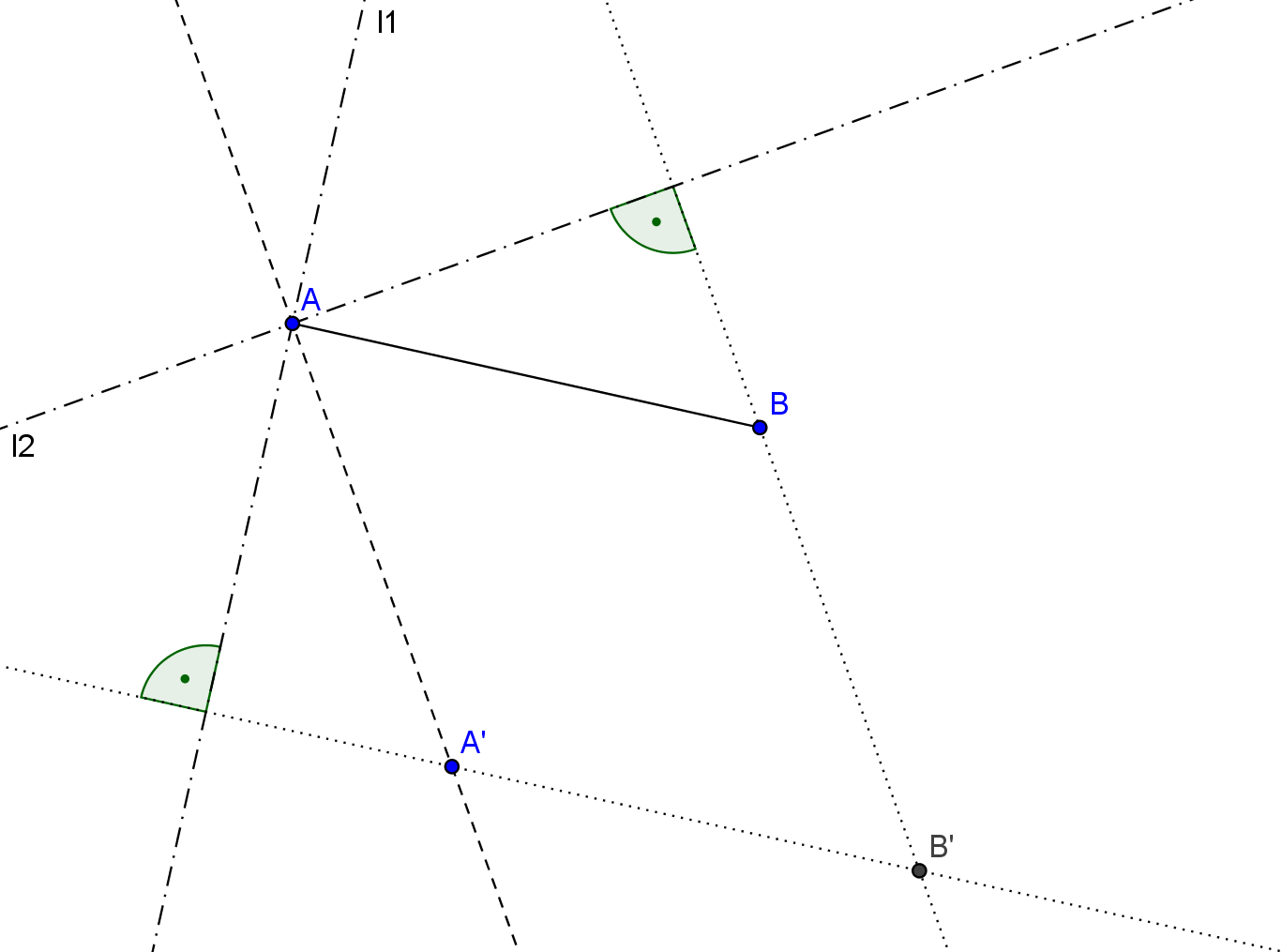
To perform a parallel translation of the line segment $AB$ such that $A$ coincides with $A'$ (see fig.2), at first the line segment $AA'$ is drawn. Then you construct both the perpendicular $l1$ through $A$ to $AB$ as well as the perpendicular $l2$ through $A$ to $AA'.$ Through $B$ you construct the perpendicular to $l2$ and through $A'$ the perpendicular to $l1.$ The auxiliary arcs and lines to construct these perpendiculars are omitted in the figure, in order to keep it clear. The last-mentioned perpendiculars intersect in $B'.$ Because $ABA'B'$ is a parallelogram, $A'B'$ has the same length and direction as $AB.$
[Show in new tab]
Performing those constructions one always starts with given points, lines or circles. Coming from these, one creates new points, lines or circles, using only the permitted operations. Often the standard starting point for ruler and compass constructions is a line segment of length $1$ or equivalently a Cartesian coordinate system with the points $(0,0)$ and $(1,0)$ marked on the $x$-axis. When constructing regular polygons one usually starts with a coordinate system with given unit circle and requires the unit circle to become the circumscribed circle of the polygon. Of course, this starting condition is also equivalent to the given line segment of length $1.$
In what follows we will mostly be concerned with the constructibility of points in a Cartesian coordinate system. Such a point is said to be constructible with ruler and compass, if its $x$-coordinate and its $y$-coordinate are constructible following Euclid's rules.
Addition and Subtraction of Coordinates of Points
We will only cope with $x$-coordinates, because $y$-coordinates are treated in the same way. Given two points with coordinates $(a,0)$ and $(b,0)$ respectively, the point with coordinates $(a+b,0)$ is easily constructed by parallel translation such that the line segment from $(0,0)$ to $(b,0)$ is shifted along the x-axis until its starting point falls upon $(a,0)$. The endpoint of the shifted line segment is then the desired point with coordinates $(a+b,0)$. This works also for negative values of $a$ or $b$ provided that the lines keep their orientation given by the starting point in the origin. The point $(a-b,0)$ is constructed by addition of the coordinates of $(-b,0)$ to the coordinates of $(a,0)$. Starting with a Cartesian coordinate system with given points $(0,0)$ and $(1,0)$ one can construct arbitrary points with integer coordinates in this manner.
Multiplication and Division of Coordinates of Points
One can multiply and divide with ruler and compass, using the intercept theorem. To keep things simple, we deal with positive values only, that is to say we construct the product or quotient of the absolute values of the coordinates and correct for the sign, by choosing the proper orientation, when shifting the result to the origin. Furthermore, we represent the points with coordinates $(a,0)$ and $(b,0)$, which we want to multiply, by lines of length $a$ and $b$, which we can place, where it is convenient.
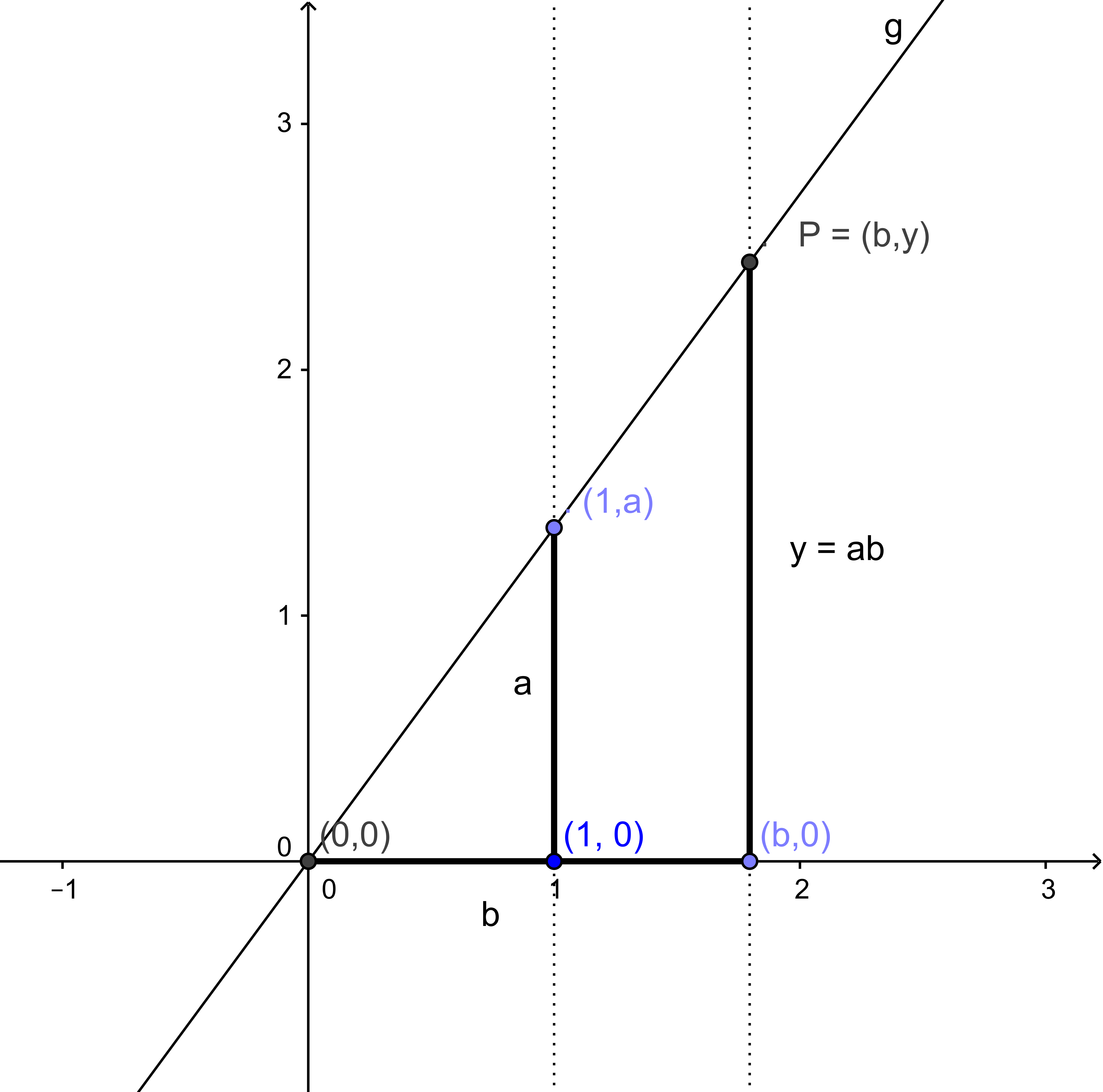
Given these two lines with length $a$ and $b$ one constructs the perpendicular to the $x$-axis through the point $(1,0)$ with length $a$ (see fig.3). Hence its endpoint has coordinates $(1,a)$. Draw the line $g$ through the origin $(0,0)$ and the point $(1,a).$ Then construct the perpendicular to the $x$-axis through the point $(b,0).$ This perpendicular intersects the line $g$ in point $P.$ The intercept theorem gives us for the $y$-coordinate of $P$: \[\frac{a}{1} = \frac{y}{b}\:{\rm ,}\] hence we have $y = ab$ and performed the multiplication of $a$ and $b$.
[Show in new tab]
The construction for the division is almost the same. You have only to take $y$ as given and $a$ as the desired result. Hence you at first construct the perpendicular to the $x$-axis through the point $(b,0)$ with length $y,$ then draw the line $g$ through its endpoint $P = (b,y)$ and the origin. The perpendicular to the $x$-axis through the point $(1,0)$ intersects the line $g$ in $(1,a).$ From the above computation we have $a = y/b$ and thus performed the divison of $y$ by $b$.
Beginning with a coordinate system with given points $(0,0)$ and $(1,0)$ one thus can construct all points, whose coordinates are fractions of integers, in other words all points with rational coordinates.
Solving Qudratic Equations
Extracting square roots or more generally solving quadratic equations with ruler and compass requires some more consideration. Without loss of generality we can assume the equation to be normalized like $x^2 + ax + b = 0,$ with $a$ and $b$ rational numbers (see for example [Conway 1996]).
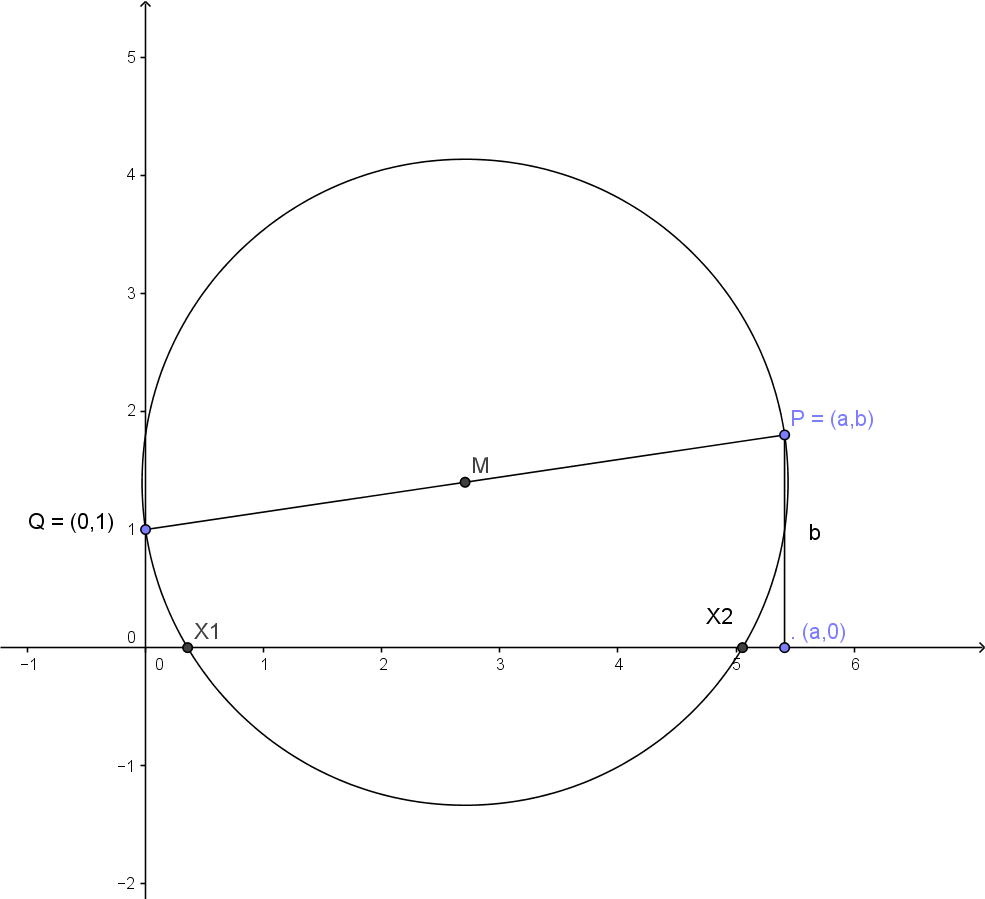
At first we construct the point $P = (a,b)$ (see fig.4) with the given rational coordinates $a$ and $b.$ Following the common practice, we will denote the set of rational numbers by $\mathbb{Q}$, so that we can write $a,b \in \mathbb{Q}$ instead.
We draw the line segment between $P$ and the point $Q = (0,1)$ and bisect the line segment $PQ$ to get its midpoint $M$. We then draw the circle with center $M$ through $P$ or $Q$. The circle intersects (if we are lucky) the $x$-axis in two points $X1$ and $X2$ whose $x$-coordinates are the solutions of the equation $x^2+ax+b=0.$
[Show in new tab]
To prove this, realize that by the Pythagorean theorem the circle has the diameter \[\sqrt{a^2 + (1-b)^2}\:{\rm .}\] The midpoint $M$ has the $x$-coordinate $a/2$ and the $y$-coordinate $b + (1-b)/2 = (1+b)/2.$ Hence we have the equation \[(x-\frac{a}{2})^2 + (y-\frac{1+b}{2})^2 = \frac{a^2+(1-b)^2}{4} \] for the circle. To find the intersection points of the circle with the $x$-axis we set $y=0$ and compute:
\[x^2 + ax + \frac{a}{4} + \frac{(b+1)^2}{4} = \frac{a^2}{4} + \frac{1-2b+b^2}{4} \] \[x^2 + ax + \frac{b^2 +2b + 1}{4} - \frac{1-2b+b^2}{4} = 0 \] \[x^2 + ax + \frac{4b}{4} = 0 \] \[x^2 +ax + b = 0\:{\rm .} \]So the $x$-coordinates of $X1$ and $X2$ are in fact the solution of the given quadratic equation. It's a good exercise to convince yourself that this method works even for the extreme cases $a=0$ or $b=0.$ You may also notice that some quadratic equations have only one (real) solution or no (real) solution at all, if the circle touches the $x$-axis in one point or does not intersect with it at all. This is especially true for $a=0$ and $b>0.$ In this case the circumference of the circle has a minimal distance from the $x$-axis of $\min(1,b)$ and thus cannot intersect with it. You may know that the solutions of $x^2+b=0$ with $b>0$ are imaginary, so this is quite correct. As a consequence, we will have to verify that the quadratic equations used for our future constructions will have real solutions.
As result of our construction we have extended the set of constructible points by those points, whose coordinates are real solutions of quadratic equations with rational coefficients. Of course, this includes especially the square roots of any non-negative rational number $b$, which are solutions of $x^2 - b = 0.$
This method to solve a quadratic equation with ruler and compass is said to be invented by the Scottish author Thomas Carlyle (1795-1881), who before turning towards literature had worked several years as a teacher of mathematics. Therefore, the circles used in this construction are called Carlyle-circles.
From the rules of Euclid it follows that all points constructed in that way can be taken as starting points for further steps in your construction. The numbers $a$ and $b$ in the above equation then are themselves of the form $p \pm \sqrt{q}$ with $p,q \in \mathbb{Q}$ and $q \geq 0,$ instead of beeing simply rational numbers. Hence the solution $x$ will contain two nested square roots. It is easily seen, that by the given method one can construct every point, whose coordinates are given by a finite expression that contains only rational numbers and nested real-valued square roots concetanated by the four basic arithmetic operations. To perform the construction in reality, the square roots are worked off from the deepest nesting level backwards. If, for example, a coordinate is given by \[ x = \sqrt{a + \sqrt{b + \sqrt{c}}} \] with $a,b,c \in \mathbb{Q},$ one constructs at first with help of the intercept theorem $c, b$ and $a$ as rational numbers. Then $\sqrt{c}$ is constructed as solution of the quadratic equation $x_1^2 - c = 0$ by the Carlyle-method. You get $x_2 = x_1 + b$ by addition and solve $x_3^2 - x_2 = 0$ again by the Carlyle-method etc. (we assume that the expressions under the square roots are always positive).
The above arguments demonstrate that one may in fact regard those chains of nested and concatenated square roots as description of a Euclidean construction to be executed with ruler and compass. That's exactly the form Gauss used to give his construction of the regular 17-gon and it's exactly the form printed by the Java program we are going to develop.
Generally, such a constuction performed by tracking backwards through a complicated expression of nested square roots will be not very elegant, to say the least. One could as well call it overwhelmingly cumbersome. But that's not our concern. To prove the constructibility, it is sufficient to give any description of the construction, simplification and facelift may be appealing tasks, but they do not improve our understanding.
So we give the following recursive definition of the term constructible point:
- Rational numbers, concatenated by the four basic arithmetic operations,
- real-valued square roots of expressions of the first kind, concatenated with each other or with expressions of the first kind by the four basic arithmetic operations,
- real-valued square roots of expressions of the second kind, concatenated with each other or with expressions of the first or second kind by the four basic arithmetic operations
- … etc. (of course only final expressions are allowed).
Without rolling out the heavy artillery of algebra, let's remind ourselves that an algebraic structure allowing all basic arithmetic operations without restrictions [1] is called a field. The rational numbers $\mathbb{Q}$ form a field as well as the real numbers $\mathbb{R}$ and the complex numbers $\mathbb{C}.$ The box above contains the rather laborious description of the fact, that you can create new fields, so called extension fields out of $\mathbb{Q}$ by adjunction of individual square roots and calculate with them as usual.
As a convenient manner of speech we will call the result of the process described within the box simply as square root expression or even as root expression.
We have shown that every root expression can be worked off with ruler and compass and thus
realized as geometrical construction. Now we want to show the inverse, namely that
the coordinates of every point, which is constructible following Euclid's rules, are given
by such root expressions – that's the reason for the caveat preliminary version
in the header of the above box.
Intersection of Lines
To do this, it is sufficient to show that the coordinates of intersection points of lines with lines, of lines with circles and of circles with circles can always be represented as root expressions.
The $x$-coordinate of the intersection point of two lines $y = m_1x + c_1$ and $y = m_2x + c_2$ is calculated by equating:
\[ m_1x + c_1 = m_2x + c_2 \] \[ x = \frac{c_2-c_1}{m_1-m_2}\:{\rm .} \] If, for example, the first line is given by two points \[ (x_1,y_1) = (p_1+\sqrt{q_1},v_1 + \sqrt{w_1}) \] and \[ (x_2,y_2) = (p_2+\sqrt{q_2},v_2 + \sqrt{w_2})\:{\rm ,} \] (we restrict ourselves to positive square roots), one calculates for $m_1$ and $c_1$ \[m_1 = \frac{y_1-y_2}{x_1-x_2}\] and \[c_1 = \frac{y_1(x_1-x_2)-x_1(y_1-y_2)}{x_1-x_2}\:{\rm .}\] Inserting the above values one gets \[m_1 = \frac{v_1 + \sqrt{w_1}-v_2 - \sqrt{w_2}}{p_1+\sqrt{q_1}-p_2-\sqrt{q_2}}\] and \[c_1 = \frac{(v_1 + \sqrt{w_1})(p_1+\sqrt{q_1}-p_2-\sqrt{q_2})-(p_1+\sqrt{q_1})(v_1 + \sqrt{w_1}-v_2 - \sqrt{w_2})}{p_1+\sqrt{q_1}-p_2-\sqrt{q_2}}\:{\rm .}\] Analogous expressions result for $m_2$ and $c_2.$ Inserted into the equation of the $x$-coordinate of the intersection, one gets a root expression of the desired form. The same is true for the $y$-coordinate.
The reason, of course, is that the equations for $x$, $m_1$ and $c_1$ are rational functions of the $x_1, x_2, y_1, y_2$ with numerator and denominator being polynomials of degree one (no squares, cubes etc.). So, inserting a valid root expression into such a function results in another valid root expression by definition.
Intersection of Circles
We restrict ourselves to perform a calculation of the coordinates of the intersection points of two circles and leave the case line intersects with circle to the reader.
At first we note that the distance of two points $(x_1,y_1)$ and $(x_2,y_2)$ is given by \[ r = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\:{\rm .} \] Inserting a square root expression for each of the coordinates will give again a nested square root expression. Thus it is allowed to write the equation for a circle with center $(x_1,y_1)$ as \[ (y-y_1)^2 + (x-x_1)^2 = r_1^2 \] with radius $r_1$ given as nested square root expression.
The intersection point of two circles is calculated from a system of two such equations with two unknowns \[(y-y_1)^2 + (x-x_1)^2 = r_1^2 \] \[(y-y_2)^2 + (x-x_2)^2 = r_2^2\:{\rm .} \] After subtracting the second equation from the first one has: \[-2yy_1 + y_1^2 +2yy_2 - y_2^2 -2xx_1 + x_1^2 + 2xx_2 - x_2^2 = r_1^2-r_2^2 \:{\rm .}\] It's important that $x^2$ and $y^2$ drop out, so that you get a linear expression in $x$, if you calculate $y$. In fact you get the equation of a line, the so called radical axis (or power line ) of the two circles:
\[y(-2y_1 + 2y_2) = r_1^2-r_2^2 - y_1^2 + y_2^2 + x(2x_1-2x_2) -x_1^2 + x_2^2 \] \[y = \frac{r_1^2-r_2^2 - y_1^2 + y_2^2 + x(2x_1-2x_2) -x_1^2 + x_2^2}{2(y_2-y_1)} \] \[y = \frac{x_1-x_2}{y_2-y_1}x+\frac{r_1^2-r_2^2 - y_1^2 + y_2^2 -x_1^2 + x_2^2}{2(y_2-y_1)} \:{\rm .}\]Inserting this into one of the equations of the circle will give a rather confusing expression, but we know that it will be a quadratic equation for $x$. Hence, the $x$-coordinate of the intersection point of two circles is the solution of a quadratic equation and the coefficients of this equation do only contain square roots of the $x_1,x_2,y_1,y_2 , r_1,r_2$ concatenated by the basic arithmetic operations. The same is true for the $y$-coordinate.
Main Theorem of Constructability
If you replace the $x_1,x_2,y_1,y_2 , r_1,r_2$ in the above expression for $x$ or $y$ by their root expressions (which must be possible, because the circles themselves were assumed to be constructed before), you finally will get an expression containing only rational numbers and nested square roots concatenated by the basic arithmetic operations. In other words: you will get a valid square root expression. In summary we can say: The permitted steps of a construction with ruler and compass following the rules of Euclid will always lead to points whose coordinates are given by expressions described above. Hence, we can replace the preliminary version given in that box by a sharpened final version:
- Rational numbers, concatenated by the four basic arithmetic operations,
- real-valued square roots of expressions of the first kind, concatenated with each other or with expressions of the first kind by the four basic arithmetic operations,
- real-valued square roots of expressions of the second kind, concatenated with each other or with expressions of the first or second kind by the four basic arithmetic operations
- … etc. (of course only final expressions are allowed).