The Complex Plane

In the previous chapter we performed our constructions in a Cartesian coordinate system whose coordinates were real numbers. The constructible points were even a subset of the real numbers, the much-quoted root expressions.

However, many construction tasks can be handled in a much smarter way, when they are performed in the complex plane. This is especially true for the constuction of regular polygons.

In Germany it depends on the federal state whether complex numbers belong to the curriculum of high schools or secondary schools. So, I cannot take for granted that German high-school students have heard about the field $\mathbb{C}$ of complex numbers. Hence I will give a crash course  about this topic in the following paragraphs, restricting myself to the facts needed for the cyclotomic theory. If Google doesn't lie, the situation for high-school students in the US and the UK is better. In these countries the topic seems to be taught at school. Anyway, I will keep the introductory paragraphs, which may be skipped by those familiar with that matter.

When I went to higschool (in the middle of the sixties) first of all the imaginary  numbers were introduced with the motivation, that one wants to solve the equation $x^2+1=0.$ In order to achieve this, the number system of the reals $\mathbb{R}$ is extended by adjoining the positive square root of $-1.$ One defines \[ \I = \sqrt{-1} \] and obtains the desired solutions of the said equation, namely $\pm\I.$

If you want to add and multiply as usual within this extended number system, you will necessarily come across expressions like $a + b\I$ with $a, b \in \mathbb{R}.$ These expressions are called complex numbers.

The rules for addition, subtraction and multiplication of these complex numbers are likewise enforced: $$ (a + b\I) + (c + d\I) = (a+c)+(b+d)\I $$ $$ (a + b\I) - (c + d\I) = (a-c)+(b-d)\I $$ and $$ (a + b\I)(c + d\I)=ac + bc\I + ad\I + bd\I^2=(ac-bd) + (bc+ad)\I $$ where $\I^2 = -1$ has been taken into account.

The rule for division is a little bit mory tricky (of course divison is only permitted for divisors not equal $0$): $$ \frac{a + b\I}{c + d\I} = \frac{(a + b\I)(c - d\I)}{(c + d\I)(c - d\I)} = \frac{(ac+bd) + (bc-ad)\I}{c^2+d^2} = \frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2}\I $$ You have to expand the fraction in order to get rid of the complex number in the denominator and obtain the normal form of a complex number.

It is easily verified that calculations with complex numbers obey the same rules (commutativity, associativity, distributivity, existence of identities and inverses) as calculations within the reals. In other words, the complex numbers form a field, which is denoted by $\mathbb{C}$. The real numbers $\mathbb{R}$ are a subfield of $\mathbb{C}$, because they can be regarded as a special kind of complex numbers, namely those of the form $a+0\I.$

For our considerations about constructibility another aspect of complex numbers is of essential importance. It's the fact that the rotation of a point around the origin $(0,0)$ has a simple arithmetical equivalent as multiplication of complex numbers.

Geometric Interpretation of Complex Numbers

Square roots of negative numbers, which had at first been used as auxiliary construction when solving cubic equations, were regarded as spooky phenomenon up to the end of the 18th century. The name imaginary  is a remnant of this attitude. To be generally accepted, a new interpretation of complex numbers as points of a plane had to be given. This geometric interpretation was invented independently by the Norwegian Caspar Wessel (1745-1818) in 1799, by the Frenchman Jean Robert Argand (1768-1822) in 1806 and finally by Gauss in 1831.

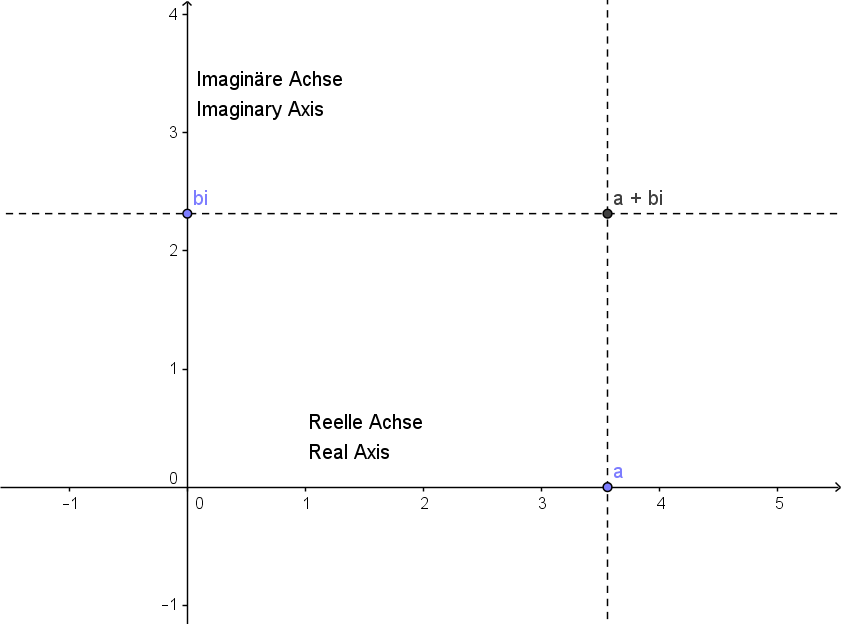
A complex number $a + b\I$ is regarded as a point of a plane with (real) coordinates $(a,b)$ (see fig.1). Hence the real numbers $a = a+0\I$ build the horizontal axis and the purely imaginary numbers $b\I = 0 + b\I$ build the vertical axis. The plane populated by the complex numbers is called complex plane  or Argand plane, in Germany the name Gaußsche Zahlenebene (Gaussian plane)  is in use as well. Unfortunately poor Wessel published his result in the proceedings of the Royal Danish Academy of Sciences and Letters in Danish. So it remained undetected for almost hundred years and no plane bears Wessel's name.

Addition of Complex Numbers

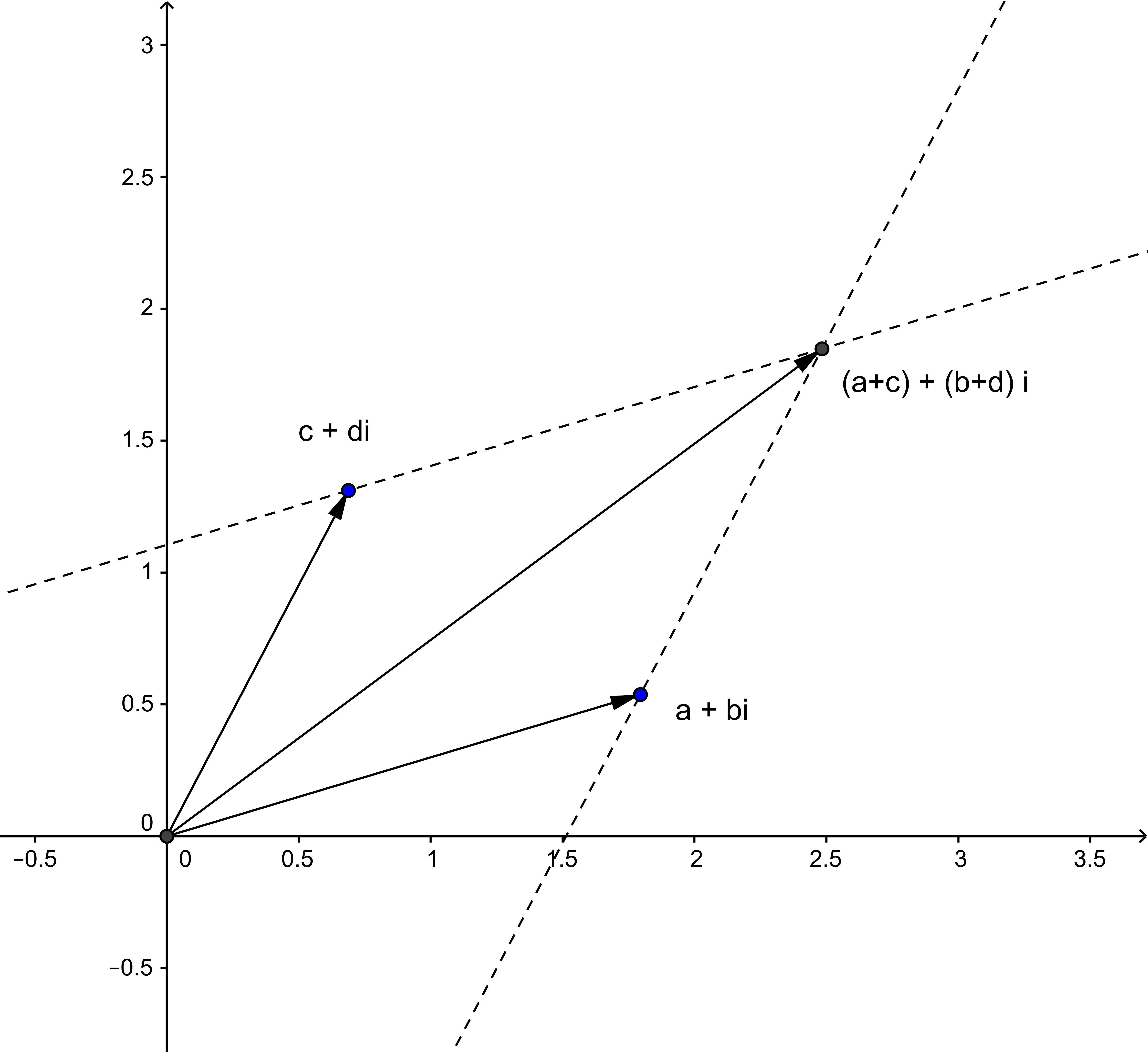
In order to visualize the arithmetical operations in the complex plane, it is helpful to imagine the complex numbers not as points  but as vectors  from the origin to the corresponding point.

To add two complex numbers $a+b\I$ and $c+d\I$ one adds separately the real and the imaginary part: \[ (a + b\I) + (c + d\I) = (a+c) + (b+d)\I\eqndot \] This is nothing else but the usual addition of vectors (see fig.2) like in a parallelogram of forces in physics. Moreover, it's a straightforward generalization of the addition of real numbers on the number line . You see immediately that the addition of complex numbers can be performed with ruler and compass.

Polar Coordinates

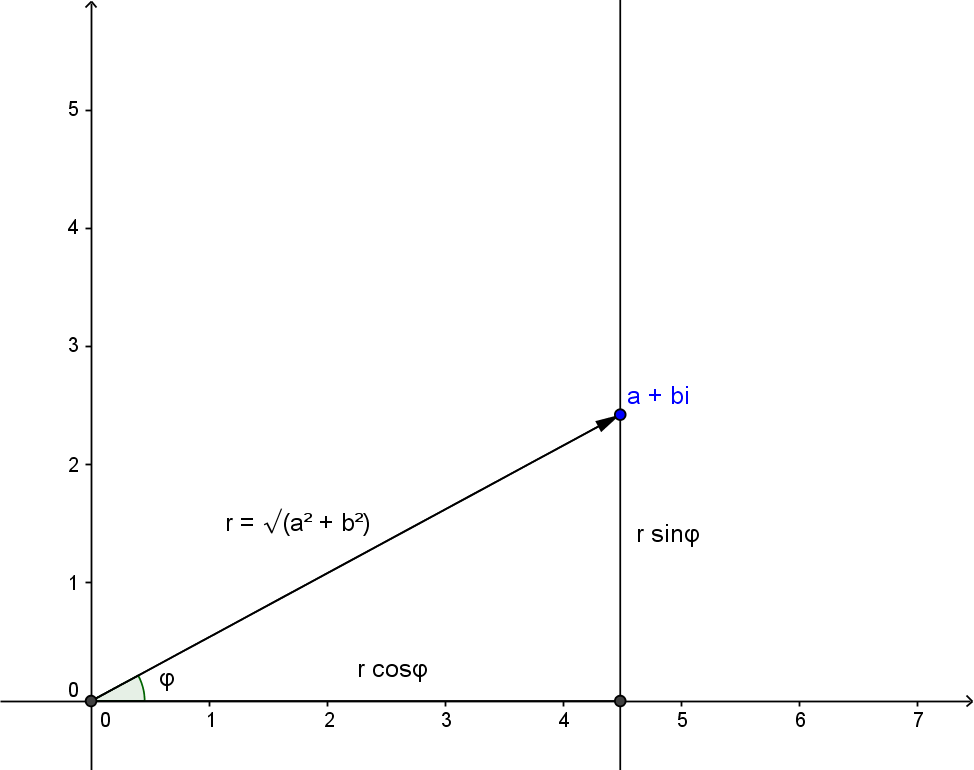
To visualize the multiplication of complex numbers one resorts to a third way to represent them. The vector from the origin to the complex number $a+b\I$ is hypotenuse in a right triangle with legs $a$ and $b.$ By Pythagoras its length is \[r = \sqrt{a^2 + b^2}\eqndot \] If you denote the angle of the vector with the real axis by $\varphi$ (see fig.3), you have \[a = r \cdot \cos \varphi\] and \[b = r \cdot \sin \varphi\eqndot\] Hence, the complex number $a+b\I$ can be uniquely represented by the pair $(r,\varphi)$ with $0 \leq \varphi \lt 360^{\circ}.$ This kind of coordinates, given by the distance from the origin and the polar angle between the vector and the real axis are called polar coordinates.

The distance from the origin is called absolute value  of the complex number \[r = \sqrt{a^2+b^2} =: |a+b\I|\eqndot\] One has \[ |a+b\I|^2 = a^2 + b^2 = (a+b\I)(a-b\I)\eqndot\] For a complex number $z = a+b\I$ its mirror image relative to the real axis is called its complex conjugate  and denoted by $\bar{z} = a-b\I.$ Hence, one can calculate the absolute value of a complex number as \[ |z| = \sqrt{z\bar{z}}\eqndot\]

As an exercise you may want to prove that the complex conjugate of the sum of two complex numbers $\overline{z_1+z_2}$ is equal to the sum of the complex conjugates $\bar{z_1}+\bar{z_2}$ and that the complex conjugate of the product $\overline{z_1z_2}$ is equal to the product of the complex conjugates $\bar{z_1}\cdot\bar{z_2}.$ Moreover, now it becomes clear, how one conceived of the trick used in connection with the division of complex numbers.

Instead of specifying the pair $(r,\varphi)$ one often writes \[a + b\I = r(\cos\varphi + \I\sin\varphi)\] or employing the famous identity of Leonhard Euler (1707-1783) \[e^{\I\varphi} = \cos\varphi + \I\sin\varphi\] one writes \[a + b\I = re^{\I\varphi}\eqndot\] Euler's identity follows from the representation of the exponential function as an infinite series (which is still taught at high school, if I am informed correctly): $$ e^x = \sum_{n=0}^\infty \frac{x^n}{n!} $$ If you insert the value $\I\varphi$ for $x$ you get: $$ e^{\I\varphi} = \sum_{n=0}^\infty \frac{\I^n\varphi^n}{n!} = 1 + \I\varphi + \frac{\I^2\varphi^2}{2!} + \frac{\I^3\varphi^3}{3!} + \frac{\I^4\varphi^4}{4!} + \dots $$ Now we have $\I^0=1, \I^1=\I, \I^2=-1, \I^3=-\I, \I^4=+1, \I^5=+\I,\dots$ and you see that the series splits into two parts for even  and odd  values of $n$: $$ e^{\I\varphi} = (1 - \frac{\varphi^2}{2!} + \frac{\varphi^4}{4!} - \dots) + \I\,(\varphi - \frac{\varphi^3}{3!} + \frac{\varphi^5}{5!} - \dots)=: c(\varphi)+\I\, s(\varphi) $$ Unfortunately it seems to be not  taught at high school that the sums in parentheses $c(\varphi)$ and $s(\varphi)$ are exactly the infinite series for $\cos\varphi$ and $\sin\varphi.$ If you never saw this representation, you are condemned to believe me. Or you verify using term by term differentiation that the functions $c(\varphi)$ and $s(\varphi)$ are solutions of the differential equations $s'(\varphi) = c(\varphi)$ and $c'(\varphi)=-s(\varphi),$ which are also solved by $\sin\varphi$ and $\cos\varphi.$ Now you have to believe only, that the trigonometric functions $\cos$ and $\sin$ are uniquely determined by that fact and by their particular boundary values $c(0)=1$ and $s(0)=0.$

Multiplication of Complex Numbers

Using polar coordinates the geometrical interpretation of the multiplication of complex numbers is easy. We already know that \[(a+b\I)(c+d\I) = (ac - bd) + (ad+bc)\I\eqndot\] Using polar coordinates \[a + b\I = u(\cos\alpha + \I\sin\alpha)\] and \[c + d\I = v(\cos\beta + \I\sin\beta)\eqncomma\] we have \[(a+b\I)(c+d\I) = uv(\cos\alpha\cos\beta - \sin\alpha\sin\beta) + uv(\cos\alpha\sin\beta + \sin\alpha\cos\beta)\I\eqndot\] Applying the well known addition theorem for trigonometric functions this is nothing else as \[(a+b\I)(c+d\I) = uv(\cos(\alpha+\beta) + \I\sin(\alpha+\beta))\eqndot\] So, to multiply complex numbers specified by polar coordinates we have to multiply the absolute values and add the polar angles. Multiplication of complex numbers is a scaling rotation .

This becomes even more obvious, if we use the representation by the exponential function: \[ue^{\I\alpha}\cdot ve^{\I\beta} = uve^{\I(\alpha+\beta)}\eqncomma\] a simple consequence of the multiplication rules for exponents.

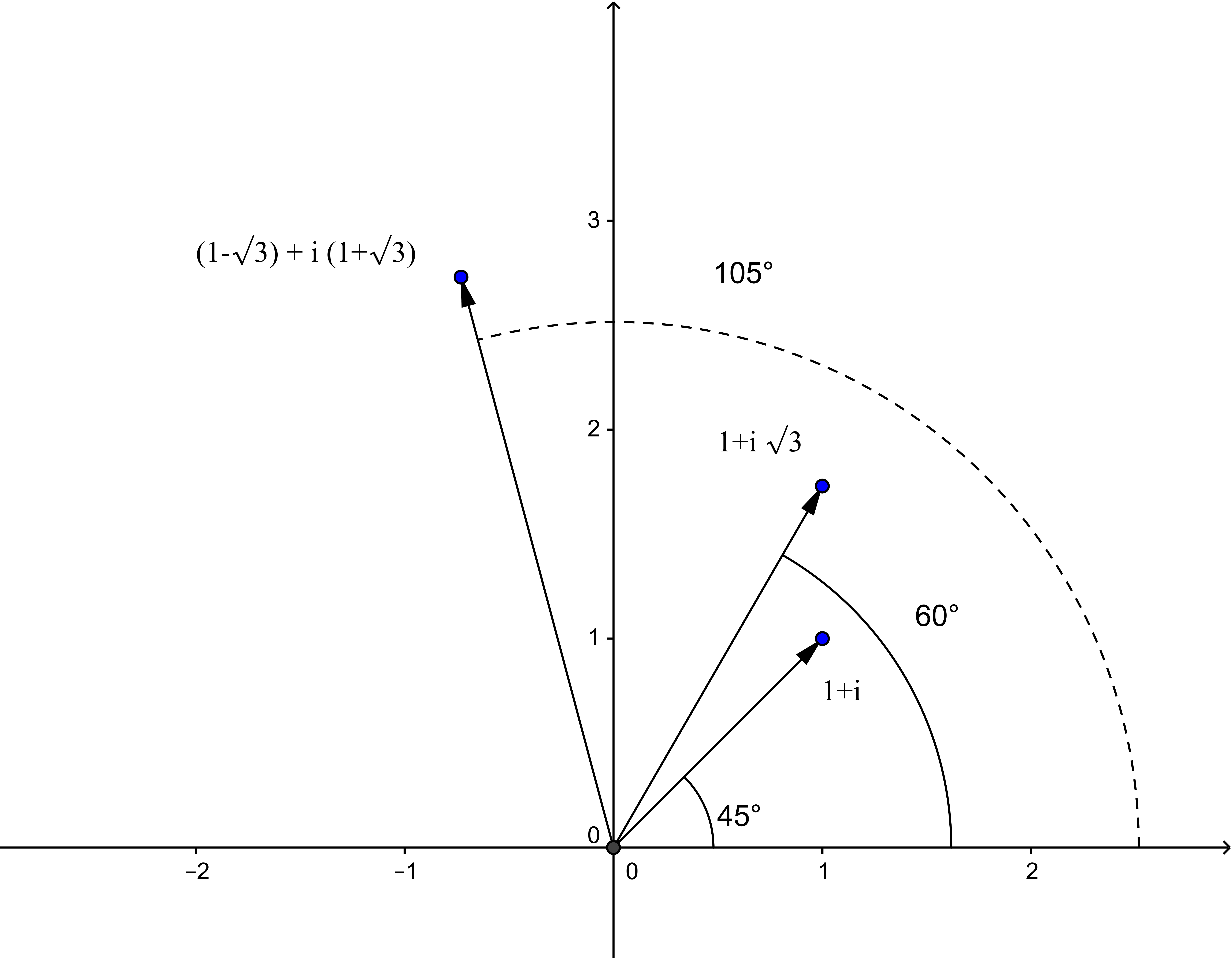
For an example have a look at fig.4. Multiplying arithmetically you get: \[(1+\I)(1+\I\sqrt{3}) = (1-\sqrt{3}) + \I(1+\sqrt{3})\eqndot\] In polar coordinates: \[1+\I = \sqrt{2}(\cos(45^{\circ})+\I\sin(45^{\circ}))\] \[1+\I\sqrt{3} = \sqrt{4}(\cos\alpha + \I\sin\alpha)\] Computing $\alpha$ from $\tan\alpha = \sqrt{3}$ we get $\alpha = 60^{\circ}.$ Multiplication of the absolute values yields: \[|1+\I|\cdot|1+\I\sqrt{3}| = \sqrt{2}\sqrt{4} = 2\sqrt{2}\] which is in agreement with the absolute value of the product: \[|(1-\sqrt{3}) + \I(1+\sqrt{3})| = \sqrt{4-2\sqrt{3}+4+2\sqrt{3}} = \sqrt{8} = 2\sqrt{2}\eqndot\] The polar angle $\varphi$ of he product can be computed: \[\tan \varphi = \frac{1+\sqrt{3}}{1-\sqrt{3}} = -(2+\sqrt{3})\eqncomma\] which is easily seen, if the fraction is expanded by $1+\sqrt{3}.$ Looking up in trigonometric tables one finds the angle $\varphi = 105^{\circ}$ for this value of $\tan\varphi,$ which (as expected) is the sum of the two polar angles of the multiplied complex numbers.

That's all you have to know about complex numbers and the complex plane to qualify you for understanding the mathematics used in the following chapters. We will almost exclusively deal with a very special kind of complex numbers, namely the complex roots of $1$ also called roots of unity. If you want to get deeper into the theory of complex numbers and learn more about their significance in mathematics and physics, you may have a look into the excellent books of Paul J. Nahin [Nahin 1998] and [Nahin 2006].