Roots of Unity

The multiplication of complex numbers becomes particularly simple, if one has complex numbers of absolute value one. In this case there is no scaling and one has only to add the polar angles resulting in a pure rotation.

In the preceding chapter we have learned that the absolute value of a complex number is its distance from the origin. Thus complex numbers with the same absolute value all lie on a circle around the origin with radius of that absolute value. Especially for complex numbers with absolute value one this is the circle with radius $1$ around the orgin, in other words the unit circle.

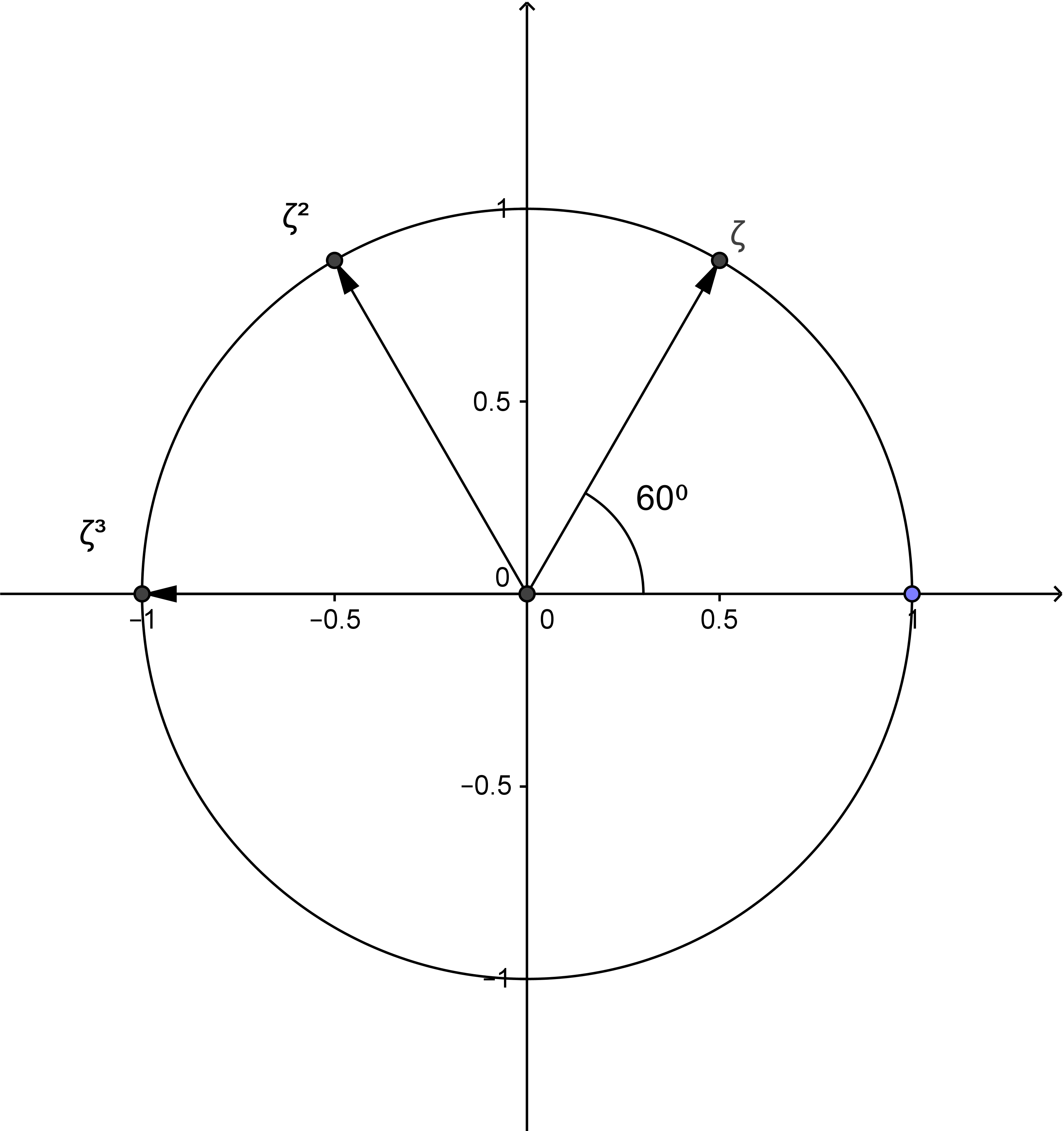
Let's take for example the complex number $\zeta$ with $|\zeta| = 1$ and let's assume that its polar angle is 60° (see fig.1). By multiplication $\zeta \cdot \zeta$ we get the complex number $\zeta^2,$ whose absolute value is also $1$ and whose polar angle is 120°. Multiplying once again with $\zeta$ gives us $\zeta^3$ with polar angle 180° etc.

By repeated multiplication we get the following table of the powers of $\zeta$ in polar coordinates, from which you can see that the complex numbers $\zeta,\dots,\zeta^6$ are uniformly spread on the unit circle, thus forming a regular hexagon : $$ \begin{align*} \zeta = \zeta^1 &= (1,60^{\circ}) \\ \zeta^2 &= (1,120^{\circ})\\ \zeta^3 &= (1,180^{\circ}) \\ \zeta^4 &= (1,240^{\circ}) \\ \zeta^5 &= (1,300^{\circ}) \\ \zeta^6 &= (1,360^{\circ}) = (1,0^{\circ}) = \zeta^0 \\ \zeta^7 &= (1,420^{\circ}) = (1,60^{\circ})= \zeta \\ \end{align*} $$

The table shows that $(\zeta^1)^6 = \zeta^6 = (1,0^{\circ}) = 1.$ But also the other powers of $\zeta$ yield $1,$ if they are taken to the 6th power: \[(\zeta^k)^6 = \zeta^{k\cdot6} = \zeta^{6\cdot k} = (\zeta^6)^k = 1^k = 1\eqndot\] A number, whose 6th power is $1$, is called 6th root of $1$, or 6th root of unity. The table above shows the six different 6th roots of unity and you see, that they are the vertices of a regular hexagon.

Regular $n$-gons

What is done for the hexagon is valid for every regular polygon as well, if its circumcircle has radius 1. The angle between adjacent rays from the center to the vertices is $360^{\circ}/n.$ From now on we will no longer measure the size of an angle in degrees but in radians, that is the length of the arc that is cut from a circle of radius 1 by the sides of the angle. We have $360^{\circ} \hateq 2\pi,$ $180^{\circ} \hateq \pi,$ $90^{\circ}\hateq \pi/2$.

It is common practice, to count the vertices of a regular ploygon counterclockwise and to start with $\zeta^0 = 1,$ the vertex on the $x$-axis. The next vertex $\zeta^1=\zeta$ corresponds to the complex number \[cos(2\pi/n) + \I\sin(2\pi/n) = e^{\frac{2\pi\I}{n}}\] and for the $k$th vertex we have \[\zeta^k = (e^{\frac{2\pi\I}{n}})^k = e^{\frac{2\pi\I k}{n}}\eqndot\] You will have noticed, that in this kind of enumeration the value $k$ is not only an index, but it's in fact the exponent, by which one has to raise $\zeta^1 = \zeta$ in order to get the $k$th vertex $\zeta^k$ as complex number. It follows immediately from the properties of the exponential function that every $\zeta^k$ is a $n$th root of unity: $$ \begin{align*} (\zeta^k)^n &= (e^{\frac{2\pi\I k}{n}})^n \\ &= e^{\frac{2\pi\I kn}{n}} \\ &= e^{2\pi\I k} = (e^{\I\pi})^{2k} = (-1)^{2k} = 1 \eqncomma\\ \end{align*} $$ where a special case of Euler's identity  for $\varphi = \pi$ has been used: \[e^{\I\pi} = \cos\pi + \I\sin\pi = -1\eqndot\] At this place, it cannot be avoided to tell, that many mathematicians rank this equation as the most beautiful  in the whole of mathematics, especially if it's written in the form: \[e^{\I\pi} + 1 = 0 \eqncomma\] because it gives an non trivial relation between the most important constants of mathematics $e, \pi, \I, 1$ and $0.$

But let's come back to the constructon of regular polygons and recapitulate the result of our considerations in compact form:

If we deal with a specific $n$-gon, or if the number of vertices is not relevant, we will omit the index $n$ of $\zeta_n^k$ and use the shorthand $\zeta^k.$

The Cyclotomic Polynomial

The $n$th roots of unity are the solutions of the equation $x^n = 1$ with $x \in \mathbb{C}$, in other words, they are the complex zeroes of the polynomial $X^n-1.$ We follow the convention to write the unknown of a polynomial in capital letters. This should indicate, that one can calculate with polynomials the same way as with whole numbers, namely add, subtract and multiply. It's said that polynomials form a ring, which is written $\mathbb{Q}[X]$ or $\mathbb{Z}[X]$, depending on whether the coefficients^[1] of the polynomial are taken from $\mathbb{Q}$ or from $\mathbb{Z}.$

One zero of the polynomial $X^n-1$ does not depend on $n$ and can be given immediately: $\zeta^0=1.$ The polynomial $X^n-1$ thus may be divided by the linear factor $X-1$ resulting in \[X^n-1 = (X-1)(X^{n-1} + X^{n-2} + \dots + X^2 + X + 1)\eqndot\] You may want to prove this by explicit multiplication. The second factor, the expression $X^{n-1}+X^{n-2}+\dots+X^2+X+1$ is called cyclotomic polynomial  ^[2], because the zeroes of this  polynomial are the crucial ones for the construction of the regular $n$-gon, the trivial zero $\zeta^0 = 1$ being given in advance anyway.

One has to be careful not to confuse the cyclotomic polynomial with the polynomial $X^n-1,$ the more so as the equation $x^n=1$ as well as $x^n-1=0$ for complex $x$ is sometimes called cyclotomic equation. Of course, all these concepts are related, and serious mistakes will be rare.

One important result shall be saved for future use: It follows from the given factorization of $X^n-1$: \[X^{n-1}+X^{n-2} +\dots+X^2+X+1 = \frac{X^n-1}{X-1}\eqndot\] Inserting the $n$th root of unity $\zeta = \zeta^1$ yields: \[\zeta^{n-1}+\zeta^{n-2}+\dots+\zeta^2+\zeta=\frac{\zeta^n-1}{\zeta-1}-1=\frac{1-1}{\zeta-1}-1=-1\eqndot\]

To illustrate this geometrically, let's have a look at the regular hexagon again. By reason of symmetry for every vertex $\zeta$ of a regular polygon the complex conjugate $\bar{\zeta}$ is a vertex as well (see fig.2). By the usual way to enumerate vertices we have $\overline{\zeta^k}=\zeta^{n-k}=\zeta^{-k}.$ If $n$ is even we have for the special case $k = n/2,$ the identity $\overline{\zeta^{n/2}} = \zeta^{n/2}.$ For the hexagon this applies to $\zeta^3$, which is the vertex at $-1$, being its own complex conjugate.

The above sum contains all roots of unity other than 1. It may be ordered in such a way as to combine every root of unity with its complex conjugate. The sum of a complex number and its complex conjugate $\zeta+\overline{\zeta}$ is always a real number and again by reason of symmetry we have for the hexagon $\zeta^1+\zeta^5 = - (\zeta^2+\zeta^4),$ leaving from the sum only the self-conjugate value $\zeta^3 = -1$.

For polygons with an odd number of vertices, we don' have an equally suggestive geometric illustration, because there is no vertex at $-1$ and the vertices are only symmetrical with regard to the real axis not with regard to the imaginary axis. However, there is a kind of physical argument, making the identity plausible at least: Interpreting the roots of unity as vectors in a parallelogram of forces, all tearing at the origin, the resulting force must be zero, because the origin is teared equally into all directions. Looking especially at the vector from the origin to the point $1,$ its force must be compensated by the sum of the forces of all the other vectors. So the sum of all vectors except the one pointing to $1$ must be a vector pointing to $-1$, and that's our result.

Elementary Symmetric Expressions

Another possibility to compute the sum of the roots of unity shall be mentioned, because we will need the method later on in another context. In addition we will gain insight into the relationship of all the roots among each other according to arithmetic criteria, to quote Gauss.

The zeroes of the cyclotomic polynomial $X^{n-1}+X^{n-2} +\dots+X^2+X+1$ are the roots of unity $\zeta, \zeta^2, \dots ,\zeta^{n-1}.$ Hence it splits into linear factors over the complex numbers: \[X^{n-1}+X^{n-2} +\dots+X^2+X+1 = (X-\zeta)(X-\zeta^2)\cdot \dots \cdot(X-\zeta^{n-2})(X-\zeta^{n-1})\eqndot\] The right side can be expanded and sorted due to powers of $X.$ For $X^{n-1}$ one takes one $X$ from each linear factor and none of the $\zeta^k,$ resulting automatically in the coefficient $1$ for $X^{n-1}.$

For $X^{n-2}$ one takes $X$ from $n-2$ linear factors and $\zeta^k$ from one linear factor for each $k,$ so one has the coefficient $-\zeta-\zeta^2-\dots-\zeta^{n-1}$ for $X^{n-2}.$ For $X^{n-3}$ one takes $X$ from every linear factor except two and from two linear factors the values $\zeta^k$ or $\zeta^l.$ So one has as coefficient of $X^{n-3}$ the sum of all possible products of two  different roots of unity: $\zeta\zeta^2 + \zeta\zeta^3 + \dots + \zeta^{n-2}\zeta^{n-1}.$

In this way every coefficient of a power of $X$ can be computed and one finally gets for the constant value 1 the product $\pm\zeta\zeta^2\cdot\dots\cdot\zeta^{n-2}\zeta^{n-1},$ with the sign depending on the fact whether $n-1$ is even or odd.

The expanded coefficients, computed in this manner and taken with positive sign, are called elementary symmetric expressions  of the $\zeta,\zeta^2,\dots,\zeta^{n-1}.$ The name is due to the fact that one may exchange every root of unity $\zeta^k$ with every other root of unity $\zeta^l$ without changing the value of the expression. In other words, the coefficients are invariant  or symmetric  under all permutations  of the roots of unity.

By equating coefficients we get the formula for the sum of the roots of unity once again, because the coefficient of $X^{n-2}$ is $1$ and on the other hand $-\zeta-\zeta^2-\dots-\zeta^{n-1}.$

Moreover, all coefficients of the cyclotomic polynomial are equal to $1$, and thus by equating coefficients we find generally that all elementary symmetric expressions of the roots of unity must equal $\pm1$.

Of course, elementary symmetric expressions of roots of unity can easily be reduced, so it may seem that we proved a triviality. For example we have for the constant term: \[\zeta\zeta^2\cdot\dots\cdot\zeta^{n-2}\zeta^{n-1} = (\zeta\zeta^{n-1})(\zeta^2\zeta^{n-2})\dots\eqncomma\] and we get only factors $\zeta^n=1$ if $n$ is odd and thus the result $+1.$ If $n$ is even one factor of value $\zeta^{n/2}$ does not find a partner, but that factor just equals $-1,$ as we have seen already for the hexagon.

Let's stay with the hexagon and equate the coefficients of $X^{n-3}$: $$ \begin{align*} 1 &= \zeta\zeta^2 +\zeta\zeta^3+\zeta\zeta^4+\zeta\zeta^5+\zeta^2\zeta^3+\zeta^2\zeta^4+\zeta^2\zeta^5+\zeta^3\zeta^4+\zeta^3\zeta^5+\zeta^4\zeta^5\\ &= \zeta^3+\zeta^4+\zeta^5+\zeta^6+\zeta^5+\zeta^6+\zeta^7+\zeta^7+\zeta^8+\zeta^9\\ &= \zeta^3+\zeta^4+\zeta^5+1+\zeta^5+1+\zeta+\zeta+\zeta^2+\zeta^3\\ &= 2(1+\zeta+\zeta^3+\zeta^5)+(\zeta^2+\zeta^4)\\ &= 2(\zeta+\zeta^5)+(\zeta^2+\zeta^4) \end{align*} $$ In the next-to-last line we inserted the value $-1$ for $\zeta^3.$ Here we get no triviality but at least a geometrical relationship, which can also be seen by strenuously watching fig.2.

Combining this with the result of equating coefficients for $X^{n-2}$ we get two equations with the two unknowns $\zeta+\zeta^5$ and $\zeta^2+\zeta^4$: $$ \begin{align*} 2(\zeta+\zeta^5)+(\zeta^2+\zeta^4) &= 1\\ (\zeta+\zeta^5) + (\zeta^2+\zeta^4) &= 0\\ \end{align*} $$ The second equation results from $\zeta+\zeta^2+\zeta^3+\zeta^4+\zeta^5=-1,$ inserting once again $-1$ for $\zeta^3$.

Solving this system of equations we get $\zeta+\zeta^5=1,$ and thus, only by a little bit of arithmetic using elementary symmetric expressions of the 6th roots of unity, we finally got a description of construction for the regular hexagon. Indeed, we have \[\cos(2\pi/6)=(\zeta+\zeta^5)/2=\frac{1}{2}\eqncomma\] as is easily seen comparing congruent triangles. Hence the $x$-coordinate of the 6th root of unity $\zeta$ is $\frac{1}{2}.$ For a construction of the regular hexagon one only has to construct the perpendicular through the point $(\frac{1}{2},0)$ to the $x$-axis, whose intersection with the unit circle gives $\zeta.$

Ok, this is no sensational result for the hexagon, but we will see soon, that sums and products of roots of unity play a crucial role when constructing other regular polygons.

You may be sure that Gauss, who was a passionate and virtuous computer, performed such calculations with roots of unity – and many more demanding ones as well – with paper and pencil by the dozen, and it was this intimate knowledge of the arithmetic of the roots of unity, which lead him to the sudden insight of the constructability of the 17-gon.

Retrospection and Outlook

Now we have reached the point, at which young Gauss arrived in 1796. However, after 200 additional years in the history of mathematics, the way for us was much les arduous. In the time of Gauss complex numbers were by no means generally accepted entities. In fact, about 30 years later, it was Gauss himself, who helped to establish them firmly in mathematics. Even Euler's identity, the basis for computations with roots of unity, was only about 48 years old at that time.

The next chapter will actually present the flash of genius of the nineteen years old Gauss, and it would even today be a flash of genius, if a student of mathematics in the 21st century, who after his or her second or third term should know by heart everything, we have presented so far, came up autonomously with this idea, that Gauss came up with, one early morning in his bed, thinking strenuously.

It is appropriate now to pause for a moment and recap, how far we got: We want to show that certain regular polygons can be constructed with ruler and compass. We have pegged the vertices of a regular $n$-gon as complex $n$th roots of unity. Hence, our task is to prove that the coordinates of certain complex roots of unity can be represented by sums and products of rational numbers and nested real square roots of such expressions.

It will suffice, to give this proof for the $x$-coordinate, because all points with this coordinate lie on a parallel to the $y$-axis. Furthermore, the roots of unity lie on the unit circle. Thus the $y$-coordinate can be constructed as intersection of the said parallel with the unit circle.

Looking at the $x$-coordinate of the root of unity $\zeta^1,$ we can calculate this coordinate by definition of the regular $n$-gon as $\cos(2\pi/n).$ On the other hand we know that the sum of a root of unity with its complex conjugate gives a real number, and especially for $\zeta^1$ in the case of the hexagon we had: \[\zeta^1 + \bar{\zeta^1} = \zeta^1 + \zeta^{n-1} = 2\cos(2\pi/n)\eqndot\] This is true for every  regular $n$-gon, simply as a consequence of the definition of the $n$th root of unity: \[\zeta^1 + \bar{\zeta^1} = \cos(2\pi/n)+\I\sin(2\pi/n)+\cos(2\pi/n)-\I\sin(2\pi/n)=2\cos(2\pi/n)\eqndot\]

For the equilateral triangle we are already done with this, and can pin down the construction description immediately, because there are only two 3rd roots of unity other than $1$, and their sum is on the one hand $-1$ and on the other hand $2\cos(2\pi/3)$. So we have for the $x$-coordinate of $\zeta_3$: $$ x = \cos(2\pi/3) = \frac{1}{2}(\zeta_3+\bar{\zeta_3})=\frac{1}{2}(\zeta_3+\zeta_3^2)=\frac{1}{2}(-1)=-\frac{1}{2}\eqndot $$ Admittedly, this is not the usual way to construct an equilateral triangle, but it works.

Hence, it will suffice, to find the desired square root expression for $\zeta^1 + \zeta^{n-1},$ a sum of two roots of unity. Combined with the fact that other sums and products of roots of unity are rational or even whole numbers, it may be supposed that it will be useful to learn more about sums and products of roots of unity. But to find the way, how these sums and products have to be formed, required strenuous thinking  even by someone like Gauss.