Gauss' Java Trip
A Mathematical Travel Report

Pentagon, Heptadecagon and 257-gon

We say nothing about the triangle and the square in this chapter.

The Pentagon

The output of the program Hermes for the regular pentagon is the following (here and in the following printouts the numerical simplification of $p_{1,0}$ and $p_{1,1}$ has been added by hand) 

% Running with arguments: 5 -tex
\[p_{0,0} = -1,000000000000\]
\[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1+\sqrt{5}}{2}\]
\[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1-\sqrt{5}}{2}\]
% 1/2 * p_{1,0} = 0.30901699437494745
% cos(2*pi/5): 0.30901699437494745
% Time used: 0.019803774sec

Rendering the output with LaTeX gives: \[p_{0,0} = -1,000000000000\] \[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1+\sqrt{5}}{2}\] \[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(p_{0,0})}}{2} = \frac{-1-\sqrt{5}}{2}\]

Fig.1: Construction of the regular pentagon
[Show in new tab]

Inserting everywhere $-1$ for $p_{0,0}$ is all we need to get the final result: \[\cos(2\pi/5) = \frac{1}{2}p_{1,0} = \frac{-1 + \sqrt{5}}{4}\]

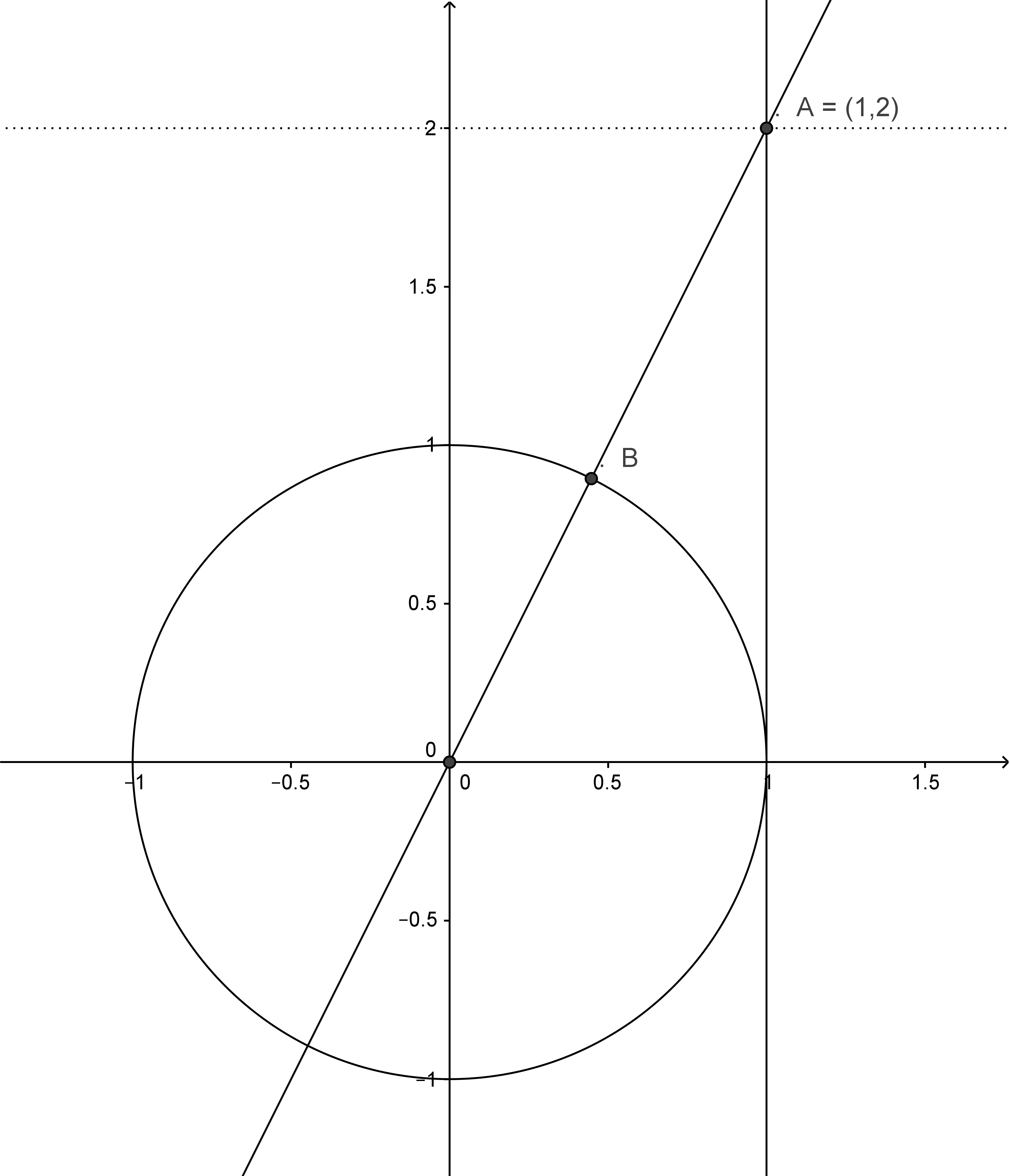
In this case, like with every other polygon construction, the first step is to extract the square root of the number of vertices, to subtract $1$ from the result, and to cut in half the latter. In case of the pentagon, we are almost done with this. Note that $\sqrt{5}$ is the length of the hypotenuse in a right triangle with legs $1$ and $2$. The subtraction of the length of the shorter leg from the hypotenuse is nothing else as the basic construction of the golden ratio (see fig.1). The $x$-coordinate of the root of unity $\zeta^1_5$ is constructed by quartering the line segment $AB$.

The Heptadecagon

I promise that the word heptadecagon will not be used any more in this text. The output of the program Hermes for the regular 17-gon is the following: 

% Running with arguments: 17 -tex
\[p_{0,0} = -1,000000000000\]
\[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1+\sqrt{17}}{2}\]
\[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1-\sqrt{17}}{2}\]
\[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\]
\[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\]
\[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\]
\[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\]
\[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\]
\[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\]
% 1/2 * p_{3,0} = 0.9324722294043557
% cos(2*pi/17): 0.9324722294043558
% Time used: 0.022387692sec

Rendered with LaTeX: \[p_{0,0} = -1,000000000000\] \[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1+\sqrt{17}}{2}\] \[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(4p_{0,0})}}{2} = \frac{-1-\sqrt{17}}{2}\] \[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\] \[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(p_{0,0})}}{2}\] \[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\] \[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(p_{0,0})}}{2}\] \[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\] \[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(p_{2,1})}}{2}\]

Doing the insertions backward, beginning with $p_{3,0}$ is a little more cumbersome, but feasible. The resulting square root expression is not too complicated:

\[p_{3,0} = \tfrac{1}{2}p_{2,0} + \tfrac{1}{2}\sqrt{p_{2,0}^2 - 4(p_{2,1})}\] $$ \begin{align*} p_{3,0} &= \tfrac{1}{4}\bigg(p_{1,0} + \sqrt{p_{1,0}^2 -4(-1)}\bigg) \\ &+ \tfrac{1}{2}\sqrt{\bigg( \frac{p_{1,0} + \sqrt{p_{1,0}^2-4(-1)}}{2}\bigg)^2 - 4\bigg(\frac{p_{1,1} + \sqrt{p_{1,1}^2 -4(-1)}}{2}\bigg)} \end{align*} $$ $$ \begin{align*} p_{3,0} &= \tfrac{1}{4}\bigg(\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2 -4(-1)}\bigg) \\ &+ \tfrac{1}{2}\sqrt{\bigg( \frac{\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2-4(-1)}}{2}\bigg)^2 - 4\bigg(\frac{\frac{-1 - \sqrt{17}}{2} + \sqrt{\big(\frac{-1 - \sqrt{17}}{2}\big)^2 -4(-1)}}{2}\bigg)} \end{align*} $$ The expressions above have been compiled within an ASCII-editor using the search and replace function. With a little more effort the roots could be further simplified, but that was not our intention. Here is the (slightly simplified) expression for $\cos(2\pi/17) = 1/2 \cdot p_{3,0}$: $$ \begin{align*} \cos(2\pi/17) &= \tfrac{1}{8}\bigg(\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2 +4}\bigg) \\ &+ \tfrac{1}{4}\sqrt{\bigg( \frac{\frac{-1 + \sqrt{17}}{2} + \sqrt{\big(\frac{-1 + \sqrt{17}}{2}\big)^2+4}}{2}\bigg)^2 - 4\bigg(\frac{\frac{-1 - \sqrt{17}}{2} + \sqrt{\big(\frac{-1 - \sqrt{17}}{2}\big)^2 +4}}{2}\bigg)} \end{align*} $$ With patience and a desk calculator the numerical value can be computed: $$ \begin{align*} \cos(2\pi/17) &= \tfrac{1}{8}\left(1.56155 + \sqrt{\left(1.56155\right)^2 +4}\right) \\ &+ \tfrac{1}{4}\sqrt{\left( \frac{1.56155 + \sqrt{\left(1.56155\right)^2+4}}{2}\right)^2 - 4\left(\frac{-2.56155 + \sqrt{\left(2.56155\right)^2 +4}}{2}\right)} \end{align*} $$ \[ \cos(2\pi/17) = \tfrac{1}{8}(1.56155 + 2.53740) + \tfrac{1}{4}\sqrt{( \frac{1.56155 + 2.53740}{2})^2 - 4(\frac{-2.56155 + 3.2498}{2})}) \] \[ \cos(2\pi/17) = \tfrac{1}{8}\cdot 4.09895 + \tfrac{1}{4}\sqrt{( \frac{4.09895}{2})^2 - 4(\frac{0.68825}{2})} \] \[ \cos(2\pi/17) = \tfrac{1}{4}(2.049475 + \sqrt{4.20034 - 1.3765}) \] \[ \cos(2\pi/17) = 0.932476 \]

Within the achievable precision the value is identical with the one computed directly from the cosines (see the output at % cos(2*pi/17):). In principle, the above square root expressions can be used directly for the construction of the 17-gon. However, in the course of time, the construction has been simplified again and again, or one has included additional conditions e.g. to use only a compass. Searching for 17-gon  oder 17-Eck  in the internet will will provide you with a lot of examples. A more systematic approach to a whole bunch of different constructions of the 17-gon, though a little bit antiquated and in German) can be found in [Mitzscherling 1913].

The 257-gon

Periods, not used for the calculation of $p_{7,0},$ have been discarded from the original output by the program Kompressor. 

% Running with arguments: 257 -tex
\[p_{0,0} = -1,000000000000\]
\[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1+\sqrt{257}}{2}\]
\[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1-\sqrt{257}}{2}\]
\[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\]
\[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\]
\[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\]
\[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\]
\[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,2} = \tfrac{p_{2,2} + \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,6} = \tfrac{p_{2,2} - \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\]
\[p_{3,1} = \tfrac{p_{2,1} - \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\]
\[p_{3,5} = \tfrac{p_{2,1} + \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\]
\[p_{3,3} = \tfrac{p_{2,3} - \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\]
\[p_{3,7} = \tfrac{p_{2,3} + \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\]
\[p_{4,0} = \tfrac{p_{3,0} + \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\]
\[p_{4,8} = \tfrac{p_{3,0} - \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\]
\[p_{4,4} = \tfrac{p_{3,4} + \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\]
\[p_{4,12} = \tfrac{p_{3,4} - \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\]
\[p_{4,2} = \tfrac{p_{3,2} + \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\]
\[p_{4,10} = \tfrac{p_{3,2} - \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\]
\[p_{4,6} = \tfrac{p_{3,6} - \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\]
\[p_{4,14} = \tfrac{p_{3,6} + \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\]
\[p_{4,1} = \tfrac{p_{3,1} + \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,9} = \tfrac{p_{3,1} - \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,5} = \tfrac{p_{3,5} + \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{4,13} = \tfrac{p_{3,5} - \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{4,3} = \tfrac{p_{3,3} + \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,11} = \tfrac{p_{3,3} - \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\]
\[p_{4,7} = \tfrac{p_{3,7} + \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{4,15} = \tfrac{p_{3,7} - \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\]
\[p_{5,0} = \tfrac{p_{4,0} + \sqrt{p_{4,0}^2 - 4(p_{4,0}+p_{4,2}+p_{4,1}+p_{4,5})}}{2}\]
\centerline{\footnotesize 2 unreferenced roots were skipped}
\[p_{5,24} = \tfrac{p_{4,8} + \sqrt{p_{4,8}^2 - 4(p_{4,8}+p_{4,10}+p_{4,9}+p_{4,13})}}{2}\]
\centerline{\footnotesize 12 unreferenced roots were skipped}
\[p_{5,1} = \tfrac{p_{4,1} + \sqrt{p_{4,1}^2 - 4(p_{4,2}+p_{4,6}+p_{4,1}+p_{4,3})}}{2}\]
\centerline{\footnotesize 2 unreferenced roots were skipped}
\[p_{5,25} = \tfrac{p_{4,9} + \sqrt{p_{4,9}^2 - 4(p_{4,10}+p_{4,14}+p_{4,9}+p_{4,11})}}{2}\]
\centerline{\footnotesize 9 unreferenced roots were skipped}
\[p_{5,23} = \tfrac{p_{4,7} + \sqrt{p_{4,7}^2 - 4(p_{4,8}+p_{4,12}+p_{4,9}+p_{4,7})}}{2}\]
\[p_{5,15} = \tfrac{p_{4,15} + \sqrt{p_{4,15}^2 - 4(p_{4,0}+p_{4,4}+p_{4,1}+p_{4,15})}}{2}\]
\centerline{\footnotesize 1 unreferenced roots were skipped}
\[p_{6,0} = \tfrac{p_{5,0} + \sqrt{p_{5,0}^2 - 4(p_{5,1}+p_{5,23})}}{2}\]
\centerline{\footnotesize 6 unreferenced roots were skipped}
\[p_{6,56} = \tfrac{p_{5,24} + \sqrt{p_{5,24}^2 - 4(p_{5,25}+p_{5,15})}}{2}\]
\centerline{\footnotesize 56 unreferenced roots were skipped}
\[p_{7,0} = \tfrac{p_{6,0} + \sqrt{p_{6,0}^2 - 4(p_{6,56})}}{2}\]
\centerline{\footnotesize 1 unreferenced roots were skipped}
% 1/2 * p_{7,0} = 0.9997011578431021
% cos(2*pi/257): 0.9997011578430937
% Time used: 0.104295518sec
Used: 40; Skipped: 89; Roots: 7144

Within the achievable precision the value computed successively by evaluation of the square root expressions is identical with the one computed directly from the cosines.

Let's torture MathJax a bit by rendering even these roots. However, we refrain from inserting the roots into one another, like we did it for the 17-gon. The reason will be given soon. Because MathJax renders LaTeX code only within a math environment, the text lines unreferenced notes were skipped stay in their raw format. Hopefully, this will not bother anybody.

\[p_{0,0} = -1,000000000000\] \[p_{1,0} = \tfrac{p_{0,0} + \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1+\sqrt{257}}{2}\] \[p_{1,1} = \tfrac{p_{0,0} - \sqrt{p_{0,0}^2 - 4(64p_{0,0})}}{2} = \frac{-1-\sqrt{257}}{2}\] \[p_{2,0} = \tfrac{p_{1,0} + \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\] \[p_{2,2} = \tfrac{p_{1,0} - \sqrt{p_{1,0}^2 - 4(16p_{0,0})}}{2}\] \[p_{2,1} = \tfrac{p_{1,1} + \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\] \[p_{2,3} = \tfrac{p_{1,1} - \sqrt{p_{1,1}^2 - 4(16p_{0,0})}}{2}\] \[p_{3,0} = \tfrac{p_{2,0} + \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,4} = \tfrac{p_{2,0} - \sqrt{p_{2,0}^2 - 4(2p_{2,0}+4p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,2} = \tfrac{p_{2,2} + \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,6} = \tfrac{p_{2,2} - \sqrt{p_{2,2}^2 - 4(4p_{2,0}+2p_{2,2}+5p_{1,1})}}{2}\] \[p_{3,1} = \tfrac{p_{2,1} - \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\] \[p_{3,5} = \tfrac{p_{2,1} + \sqrt{p_{2,1}^2 - 4(5p_{1,0}+2p_{2,1}+4p_{2,3})}}{2}\] \[p_{3,3} = \tfrac{p_{2,3} - \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\] \[p_{3,7} = \tfrac{p_{2,3} + \sqrt{p_{2,3}^2 - 4(5p_{1,0}+4p_{2,1}+2p_{2,3})}}{2}\] \[p_{4,0} = \tfrac{p_{3,0} + \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\] \[p_{4,8} = \tfrac{p_{3,0} - \sqrt{p_{3,0}^2 - 4(2p_{3,0}+p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,5})}}{2}\] \[p_{4,4} = \tfrac{p_{3,4} + \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\] \[p_{4,12} = \tfrac{p_{3,4} - \sqrt{p_{3,4}^2 - 4(p_{3,0}+2p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,1})}}{2}\] \[p_{4,2} = \tfrac{p_{3,2} + \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\] \[p_{4,10} = \tfrac{p_{3,2} - \sqrt{p_{3,2}^2 - 4(p_{3,0}+2p_{3,4}+2p_{3,2}+p_{3,6}+2p_{3,7})}}{2}\] \[p_{4,6} = \tfrac{p_{3,6} - \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\] \[p_{4,14} = \tfrac{p_{3,6} + \sqrt{p_{3,6}^2 - 4(2p_{3,0}+p_{3,4}+p_{3,2}+2p_{3,6}+2p_{3,3})}}{2}\] \[p_{4,1} = \tfrac{p_{3,1} + \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,9} = \tfrac{p_{3,1} - \sqrt{p_{3,1}^2 - 4(2p_{3,6}+2p_{3,1}+p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,5} = \tfrac{p_{3,5} + \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{4,13} = \tfrac{p_{3,5} - \sqrt{p_{3,5}^2 - 4(2p_{3,2}+p_{3,1}+2p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{4,3} = \tfrac{p_{3,3} + \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,11} = \tfrac{p_{3,3} - \sqrt{p_{3,3}^2 - 4(2p_{3,0}+p_{3,1}+2p_{3,5}+2p_{3,3}+p_{3,7})}}{2}\] \[p_{4,7} = \tfrac{p_{3,7} + \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{4,15} = \tfrac{p_{3,7} - \sqrt{p_{3,7}^2 - 4(2p_{3,4}+2p_{3,1}+p_{3,5}+p_{3,3}+2p_{3,7})}}{2}\] \[p_{5,0} = \tfrac{p_{4,0} + \sqrt{p_{4,0}^2 - 4(p_{4,0}+p_{4,2}+p_{4,1}+p_{4,5})}}{2}\] \centerline{\footnotesize 2 unreferenced roots were skipped} \[p_{5,24} = \tfrac{p_{4,8} + \sqrt{p_{4,8}^2 - 4(p_{4,8}+p_{4,10}+p_{4,9}+p_{4,13})}}{2}\] \centerline{\footnotesize 12 unreferenced roots were skipped} \[p_{5,1} = \tfrac{p_{4,1} + \sqrt{p_{4,1}^2 - 4(p_{4,2}+p_{4,6}+p_{4,1}+p_{4,3})}}{2}\] \centerline{\footnotesize 2 unreferenced roots were skipped} \[p_{5,25} = \tfrac{p_{4,9} + \sqrt{p_{4,9}^2 - 4(p_{4,10}+p_{4,14}+p_{4,9}+p_{4,11})}}{2}\] \centerline{\footnotesize 9 unreferenced roots were skipped} \[p_{5,23} = \tfrac{p_{4,7} + \sqrt{p_{4,7}^2 - 4(p_{4,8}+p_{4,12}+p_{4,9}+p_{4,7})}}{2}\] \[p_{5,15} = \tfrac{p_{4,15} + \sqrt{p_{4,15}^2 - 4(p_{4,0}+p_{4,4}+p_{4,1}+p_{4,15})}}{2}\] \centerline{\footnotesize 1 unreferenced roots were skipped} \[p_{6,0} = \tfrac{p_{5,0} + \sqrt{p_{5,0}^2 - 4(p_{5,1}+p_{5,23})}}{2}\] \centerline{\footnotesize 6 unreferenced roots were skipped} \[p_{6,56} = \tfrac{p_{5,24} + \sqrt{p_{5,24}^2 - 4(p_{5,25}+p_{5,15})}}{2}\] \centerline{\footnotesize 56 unreferenced roots were skipped} \[p_{7,0} = \tfrac{p_{6,0} + \sqrt{p_{6,0}^2 - 4(p_{6,56})}}{2}\] \centerline{\footnotesize 1 unreferenced roots were skipped}

On the website [Winter 2011] you find a link to a video, showing the construction of a 257-gon with aid of the geometry software Geogebra. Also Wikipedia presents an animation of the construction of a regular 257-gon.

It may be interesting, to comment shortly on the line Roots: 7144 in the output of the program Kompressor. The program counts, how many square roots would occur in the final expression, if all replacements of the $p_{m,n}$ would have taken place, like we did it above in case of the 17-gon. This makes clear, why we abstain from this job here. The value 7144 differs from the value given in [Trott 2000]. Trott speaks about 5133 roots. My only explanation is, that Mathematica® is superior in simplifying the expressions arithmetically. Remember, that we already classified the procedure simplify of Hermes as superficial. However, it may also be that the code of Kompressor is buggy. If you detect an error, don't hesitate to drop me a note.