Java Programs
Here you will find the Java programs, that have been mentioned on other pages of the Ja:Mathe! site. All jar files may be downloaded and used for free. The programs have been tested under Linux and Windows. Unfortunately, I have no access to a Mac, hence I can say nothing about the usability on this platform. For some of the programs I publish also the sources. These may likewise be downloaded, compiled and modified.
The programs are of varying quality. Some are primitive console applications, written ad hoc to verify a certain numerical result, others are more elaborated and provide a graphical user interface or a helpfile.
To run the Java programs, it is necessary to install the Java® SE Runtime Environment (JRE) on your computer. Unfortunately, several Linux distributions have a so called openjdk preinstalled, which in most cases is out-of-date. This should be deinstalled by sudo apt-get remove --purge openjdk*, and the original JRE by Oracle® should be installed. The latter is found at webupd8team and some other sites.
Mappings of the Complex Plane
The motivation to write this program came by reading the book Algebra by Michael Artin. In the chapter about the fundamental theorem of algebra a very ostensive proof is sketched.
[Show in new tab]
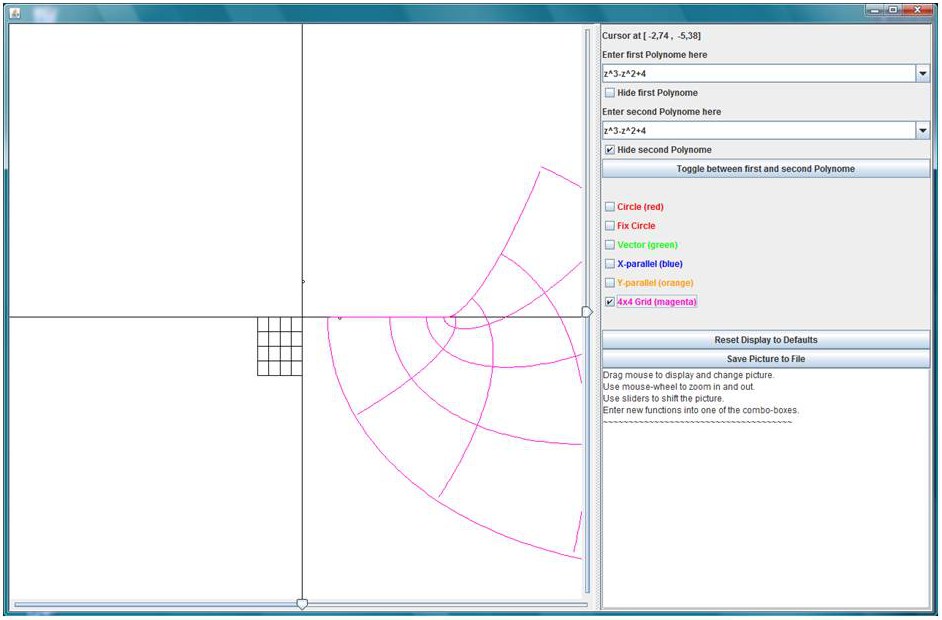
Look at the image of a circle in the complex plane mapped by a non constant polynomial with non vanishing constant term. If the circle to be mapped is very large, the highest power of the polynomial dominates the mapping: the image of the circle is a closed curve winding around the origin in great distance. If the circle to be mapped is very small, the constant term dominates: the image of the circle is mapped onto a closed curve winding around the point representing the constant term in very small distance.
To make this plausible, write the complex number $z$ in polar coordinates: $$ z = r e^{\I\varphi} $$ Then we have $r \ge 0$, $r \in \mathbb{R}$ and for the powers it holds $$ z^n = r^n e^{n\I\varphi} $$ The exponentiation expands the radius for $r \gt 1$ (a circle becomes larger) and it shrinks the radius for $r \lt 1$ (a circle becomes smaller). The term $e^{\I\varphi}$ causes the $n$-fold winding of the image around the origin or the constant term respectively.
If you shrink a very large circle continuously to a very small one, the image curves will change continuously as well. Because the image curve comes from very far away and transforms to a tiny curve around the constant term, it must pass over the origin at one moment [1] – and voila! We have proved the fundamental theorem of algebra.
Of course, this is only a sketch of a proof. In Artin's book the matter is explored in much more detail. For example you have to study the effects of the powers $a_kz^k$ with $0 \lt k \lt n$ on the image of a circle.
With help of the program you may study the images of different geometric figures (circles, grids, lines etc.) under a polynomial map in the complex plane. The figures may be scaled and moved with the mouse, so one gets a vivid impression, how the image curve expands, shrinks or passes over the origin.
To install the program, it suffices to unpack the file Polynome.zip into an arbitrary directory on your computer. If the JRE has been correctly installed, the program may be started by double clicking on the jar file (with Linux you may have to create a program starter, or you may start it from a console). The sources (Polynome.java, Complex.java) are published as well, but no further documentation is provided.
Polygon Constructions
It's rather about two programs Hermes and Kompressor, where the only purpose of the second is, to compress the output of the first.
The program Hermes computes the square root expressions, needed for the construction of the regular pentagon, the 17-gon, the 257-gon and the 65537-gon. The mathematical foundation is discussed in length within the scope of a kind of eBook Gauss' Java Trip on this site. In particular, the used algorithms are described in detail in chap.6. In that chapter you will also learn, how to install and run the said programs.
The sources and the jar files can be downloaded from here:
Both of the programs are Java console applications, there is no fancy graphical user interface. Both programs deliberately have a Spartan design, in order not to drown the important algorithms in a sea of trivialities. So even output to a file is abandoned and the lists are printed to System.out (of course Kompressor cannot avoid input from a file). Consequently, it is strongly recommended, to redirect the output stream to a file, if the calculations for the 65537-Eck are done.
Siblings and Partners
The program Mischpoke belongs definitely to the mentioned primitive ad hoc programs. It had been written originally in Java, to check the computations performed in the article The Engagement Party, Because it's so primitive, I have ported it to JavaScript, so you may play around with it on-line. In order to avoid conflicts between the JavaScript of MathJax and the JavaScript of the program, it has been outsourced to a separate page. You will find it ⇒ here.
A Solar System Simulator
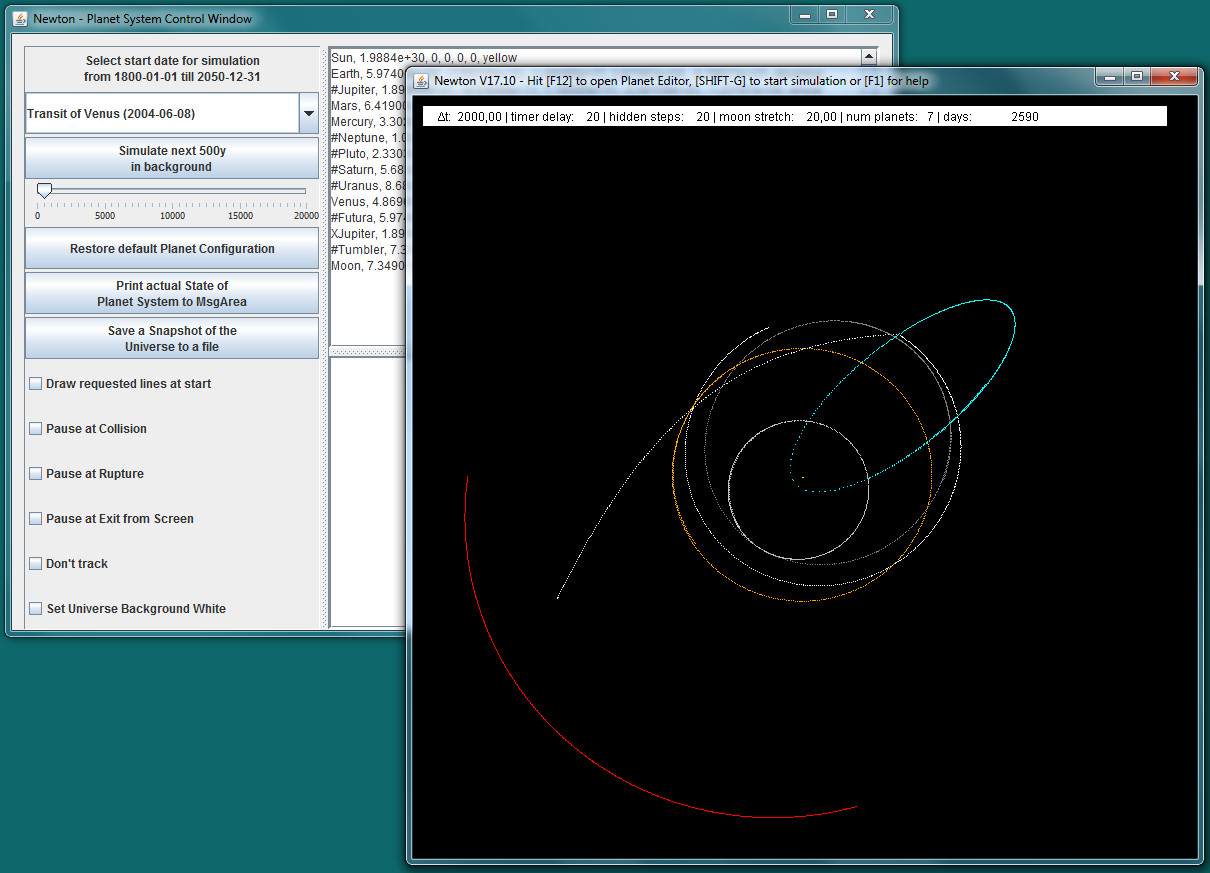
The program Newton simulates the motion of planets in the Solar system. However, you are not restricted to existing objects but may also specify fictional planets, e.g. a mirror-symmetrical twin-planet of the Earth, and watch their movement (if you read the Mathematical Marginal Urmel's Twin Planet on this site, you know the origin of that idea).
[Show in new tab]
Over time several other functions have been built into the program, have a look at the Help File for more information. Of course, the program is no sophisticated planetarium program like Stellarium, but it comes along with the source files, which you may copy, modify and compile as you like it.
To install the program, download the file Newton.zip and unpack it into an arbitrary folder on your computer. Then you may start the program by double-clicking on the file Newton.jar (with Linux you may have to create a program starter, or you may start it from a console). You will find more details about installation and operation of the program in the said help file. The source files are found here:
Calendrical Calculations
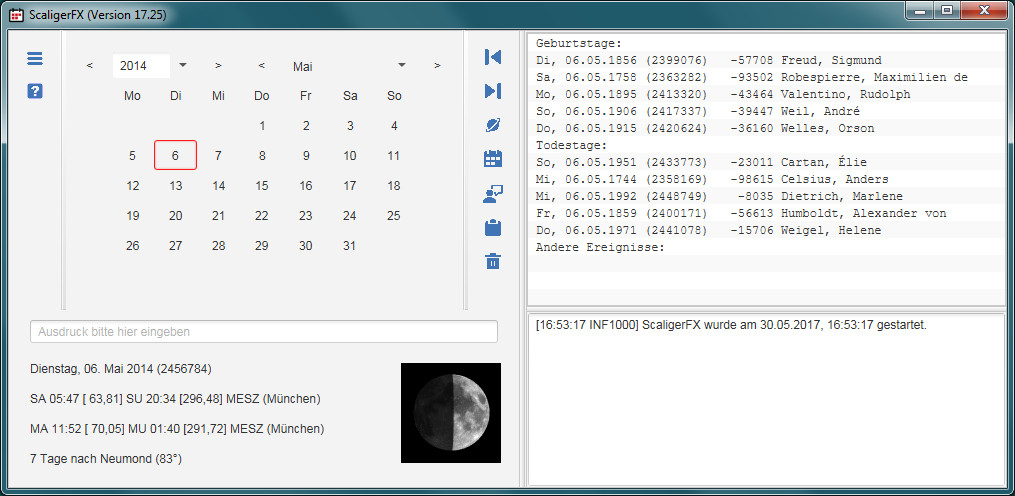
The program ScaligerFX [2] is a calendar program, which rests upon the Julian day count, invented by J. J. Scaliger in 1583. It permits a lot of different calculations with dates.
[Show in new tab]
So you may find out with a few clicks, when your age will exceed the number of days, Euler lived on earth, or you may stagger a friend of yours by congratulations to his or her 20000th day of life, or you get stunned by the fact, that the age of the famous number theorist Igor Rostislawowitsch Schafarewitsch (or Shafarevich in English transliteration), who passed away in January 2017, is 34230 days, a number that splits into the prime factors $2 \cdot 3 \cdot 5 \cdot 7 \cdot 163$ (the significance of 163 is discussed in the article Heegner number in Wikipedia).
Several files with birthdays and obits of prominent persons (extracted from Wikipedia) belong to the program. These files may be edited, to reflect your own opinion with regard to the prominence of people.
The program is equipped with two helpfiles (German and English) as PDF:
I do not publish sources of this program, because it's a rather bulky project with about 5100 lines of code. Furthermore, the interesting mathematics is hidden within the Java SE8 Date-and-Time-API and within the package org.threeten.extra.chrono.JulianChronology. The latter may be used freely, but the copyright is not mine: [(c) 2007-present, Stephen Colebourne & Michael Nascimento Santos]. Because the program ScaligerFX depends on JavaFX, an up-to-date JRE (Java SE Runtime Environment 8u40 or higher) has to be installed on your computer.
To install the program, the file Scaliger.zip has to be downloaded and unpacked into an arbitrary directory on your computer. If the JRE has been correctly installed, the program may be started by double clicking on Scaliger.jar (with Linux you may have to create a program starter, or you may start it from a console). More about the configuration of the program can be found within the aforesaid helpfiles.