Die Verlobungsfeier
Ein Brautpaar möchte seine Verlobung groß feiern. Es sollen alle Geschwister der Braut und des Bräutigams eingeladen werden, sowie deren jeweilige Ehepartner bzw. Lebensgefährten, zusätzlich alle Geschwister dieser Ehepartner bzw. Lebensgefährten, sowie deren Ehepartner bzw. Lebensgefährten und so fort, d.h. deren Geschwister nebst ihren Ehepartnern usw.
Mit wieviel Gästen müssen (oder dürfen) die beiden im Mittel rechnen, wenn man von den Familiengrößen und der Singlequote ausgeht, wie sie in der Bundesrepublik momentan (2005-2010) gegeben ist. Der Einfachheit halber machen wir die (unrealistische) Annahme, dass in der gesamten Mischpoke keine Minderjährigen vorkommen und dass auch niemand gestorben ist (womöglich unter Zurücklassung eines verwitweten Partners), dass also durchgängig die Singlequote von 43% gilt, wie wir der Wikipedia (Stand 2010) entnehmen.
Für die durchschnittlichen Familiengrößen legen wir ebenfalls die Angaben aus der Wikipedia auf Basis des Mikrozensus 2005 zugrunde
| Kinderzahl | Anteil |
| 1 | 52 |
| 2 | 36 |
| 3 | 9 |
| 4 | 2 |
| 5 | 0.6 |
| 6 | 0.2 |
| 7 | 0.08 |
| 8 | 0.03 |
| 9 | 0.014 |
| 10 | 0.006 |
| >10 | 0.005 |
Der prozentuale Anteil bezieht sich dabei auf Haushalte mit Kindern. Kinderlose Haushalte sind für unsere Überlegungen irrelevant, weil ein Ehe- bzw. Lebenspartner notwendig zu einem Haushalt mit Kindern gehört oder irgendwann gehört hat.
Wir wollen nun herausfinden, mit welcher Wahrscheinlichkeit zu der Feier 0 Gäste, 1 Gast, 2 Gäste usw. eingeladen werden müssen. Dazu veranschaulichen wir das jeweilige Beziehungsgeflecht durch eine Art Feynman-Diagramm: Zwei Personen, die durch eine Partnerschaft verbunden sind, sollen dabei durch eine gewellte Linie (ein Photon) verbunden sein, Geschwister durch eine Linie mit Pfeil (Fermion).
Für das Brautpaar selbst, das ja bei der Ermittlung der Gäste nicht mitgezählt wird, verwenden wir zur besseren Unterscheidung als Verbindung ein Gluon:
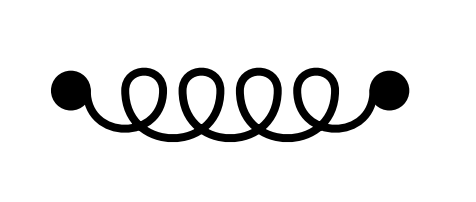
|
Hat jeder der beiden Partner ein unverheiratetes Geschwister, hat man:
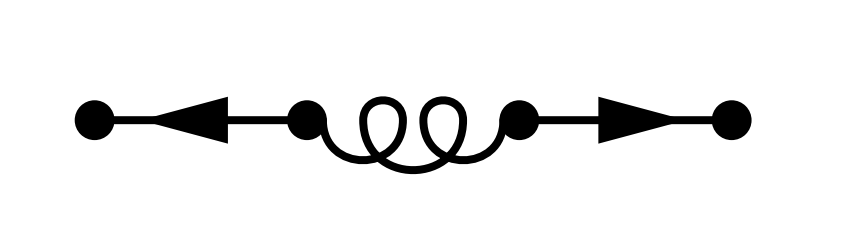
|
Hat einer zwei unverheiratete Geschwister und einer ein Geschwister, das ein Einzelkind geheiratet hat, kommt man auf
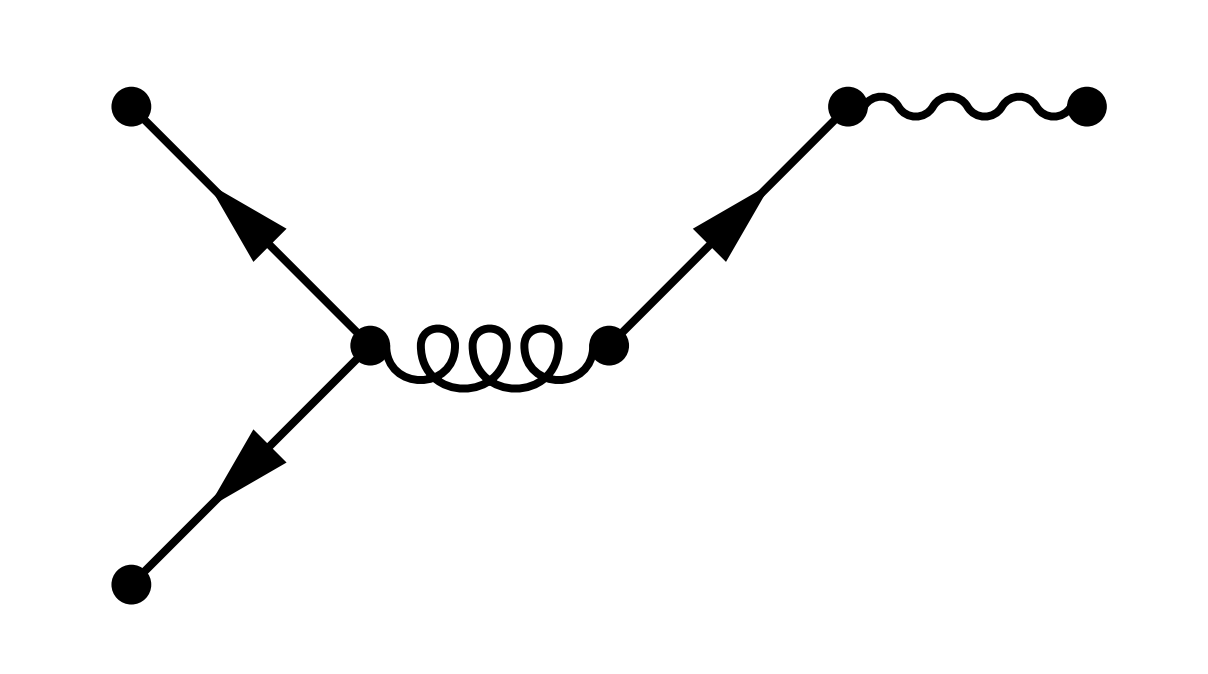
|
Die Regel ist, dass von einem Punkt immer nur ein Photon bzw. Gluon ausgehen darf (keine Bigamie) und dass ein Punkt, bei dem ein Fermion ankommt, mit keinem weiteren Fermion verbunden sein darf (Geschwister werden nur einmal gezählt) .
Wie bei den echten Feynman-Diagrammen, kann man die Wahrscheinlichkeit für eine solche Konfiguration errechnen, indem man die einzelnen Verbindungen entsprechend bewertet und miteinander multipliziert. Dabei darf man natürlich nicht vergessen, auch leere Verbindungen (bei Singles oder Einzelkindern) mit ihrer Wahrscheinlichkeit zu berücksichtigen. Ausnahme ist die Partner-Verbindung des Brautpaares selbst, deren Wahrscheinlichkeit aufgrund der Voraussetzung gleich 100% ist.
Für das erste Diagramm (Heirat zweier Einzelkinder) hat man:
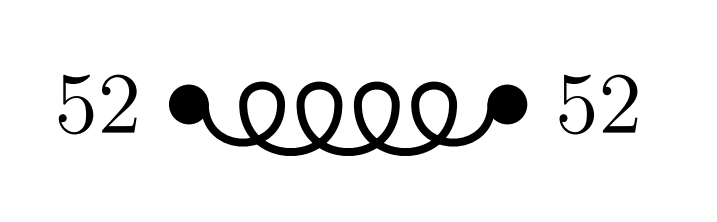
|
und somit eine Wahrscheinlichkeit von $52\%\times52\% = 27\%$. In $27\%$ aller Fälle müssen die Brautleute niemanden einladen!
Für das zweite Diagramm errechnet sich:
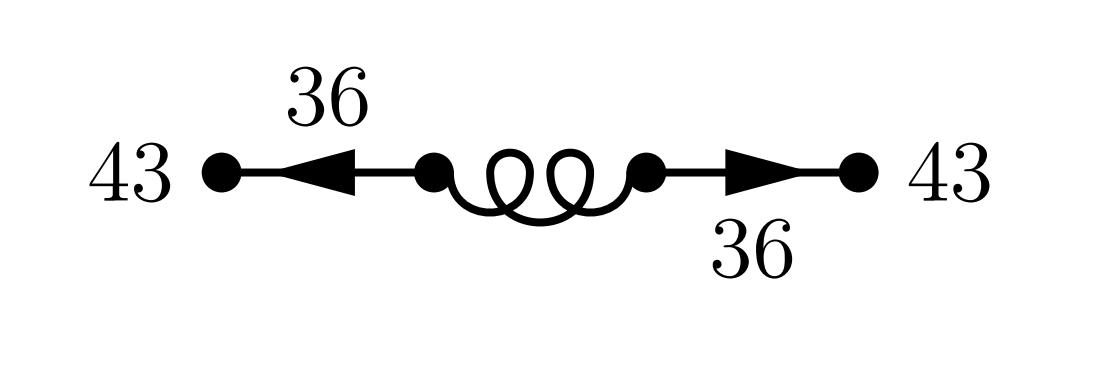
|
Die Wahrscheinlichkeit, dass ein Partner ein Geschwister hat, ist $36\%,$ die Wahrscheinlichkeit, dass dieses Geschwister Single ist, ist $43\%.$ Die Gesamtwahrscheinlichkeit für diese Konfiguration (bei der zwei Personen einzuladen wären) ist \[43\%\times36\%\times36\%\times43\%=2.4\%. \] Um unsere Aufgabe zu lösen, müssen wir folglich alle möglichen Feynman-Diagramme aufzeichnen, aus denen sich eine bestimmte Anzahl von Gästen ergibt, für jedes Diagramm die Wahrscheinlichkeit ausrechnen und diese Werte summieren. Damit erhalten wir die Gesamtwahrscheinlichkeit, dass genau diese Anzahl von Gästen einzuladen ist. Für 0 Gäste haben wir das oben schon erledigt und sind auf $27\%$ gekommen, denn es gibt in diesem Fall nur genau die eine Konfiguration. Exerzieren wir die Fälle für einen Gast, zwei Gäste bzw. 3 Gäste durch: Bei genau einen Gast haben wir das Diagramm
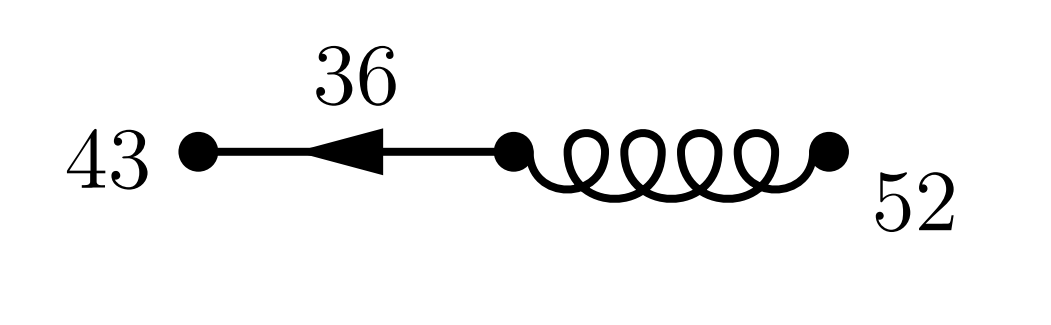
|
sowie dessen Spiegelbild
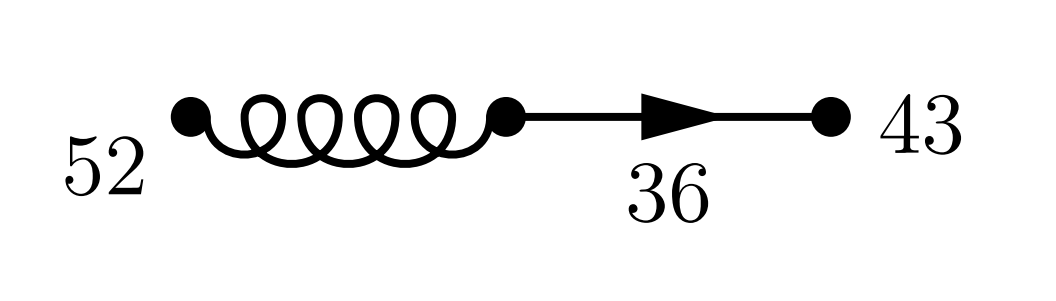
|
Für beide Konfigurationen errechnen wird die Wahrscheinlichkeit mit \[ 36\%\times 43\%\times 52\%=8\% \] Die Gesamtwahrscheinlichkeit, dass genau ein Gast kommt ist also $16\%$ Man sieht hier, dass es zu jeder nicht selbst symmetrischen Konfiguration auch immer die am Gluon gespiegelte Konfiguration mit gleicher Wahrscheinlichkeit gibt. In Zukunft führen wir derart gespiegelte Feynman-Diagramme nicht eigens auf, sondern rechnen nur ihre Wahrscheinlichkeit mit dem Faktor $2$ ein. Für zwei Gäste gibt es naturgemäß mehr Möglichkeiten, zum einen das oben als Beispiel erwähnte Diagramm mit je einem Single-Geschwister:

|
Dieses Diagramm ist symmetrisch und geht daher mit einer Wahrscheinlichkeit von $2.4\%$ nur einmal ein. Das zweite Diagramm könnte man mit Einzelkind heiratet in Dreierfamilie ein beschreiben:
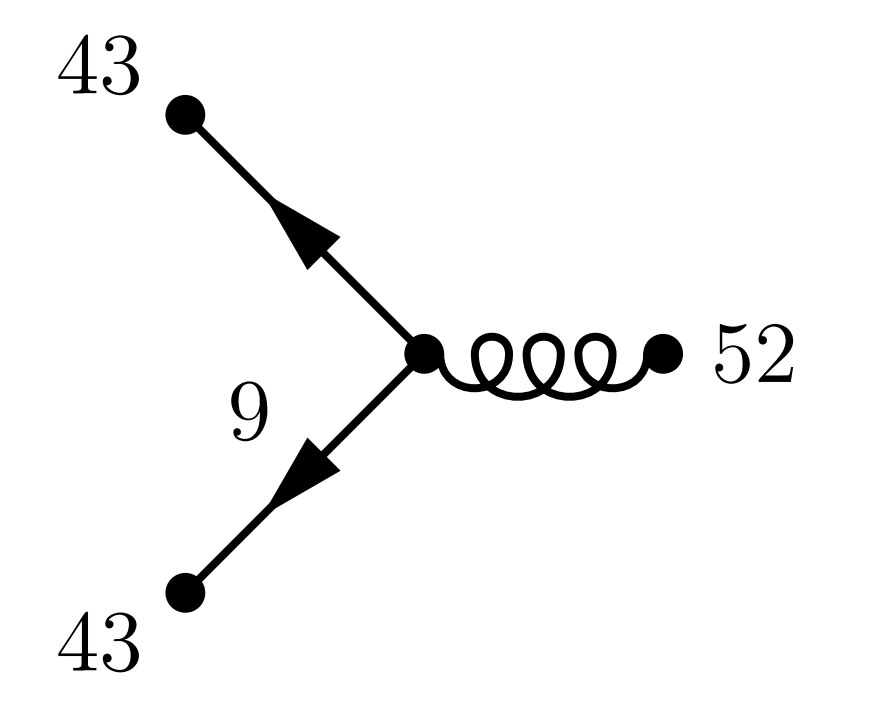
|
Hier errechnet sich die Wahrscheinlichkeit mit \[9\%\times 43\% \times 43\% \times 52\% = 0.86\%, \] die in die Gesamtsumme mit dem Faktor $2$ eingeht, weil es dazu eine gespiegelte Konfiguration gibt. Man beachte, dass die Wahrscheinlichkeit für die Existenz von zwei Geschwistern ($9\%$) natürlich nur einmal in die Rechnung eingeht und nicht etwa für jedes des beiden Geschwister, während die Tatsache, dass beide Geschwister Singles sind ($43\%$) bei jedem der Geschwister zu berücksichtigen ist. Das dritte Diagramm (Geschwister ist mit Einzelkind verheiratet ) sieht wie folgt aus:
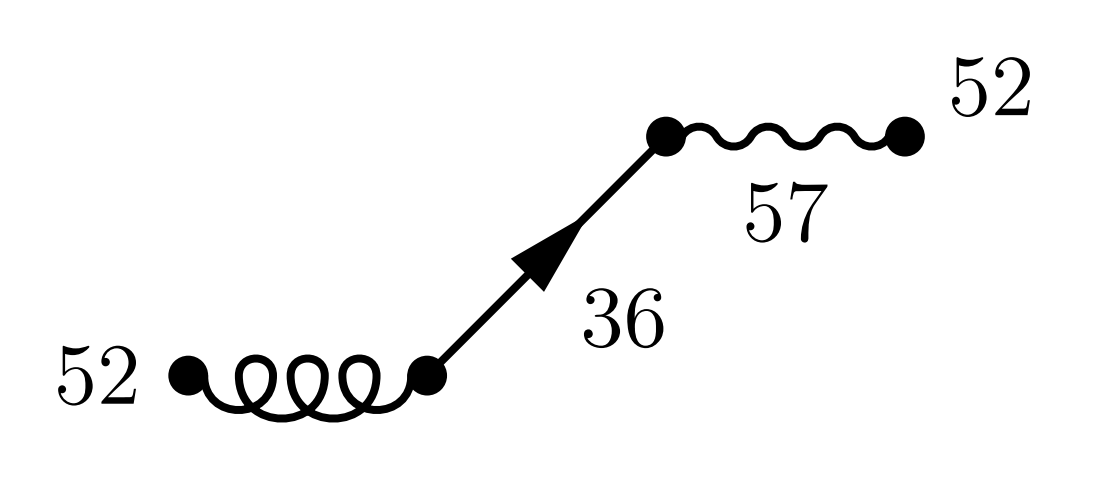
|
Auch hierzu existiert eine symmetrische Konfiguration, so dass die Wahrscheinlichkeit von \[ 52\% \times 36\% \times 57\% \times 52\% = 5.5\% \] zwei mal zu berücksichtigen ist. Insgesamt ergibt sich für genau zwei Gäste eine Wahrscheinlichkeit von \[ 2.4\% + 2\times 0.86\% + 2\times 5.5\% = 15.1\% \] Für drei Gäste wird der Prozess schon recht aufwendig. Wir listen hier nur die Diagramme ohne weitere Kommentare auf:
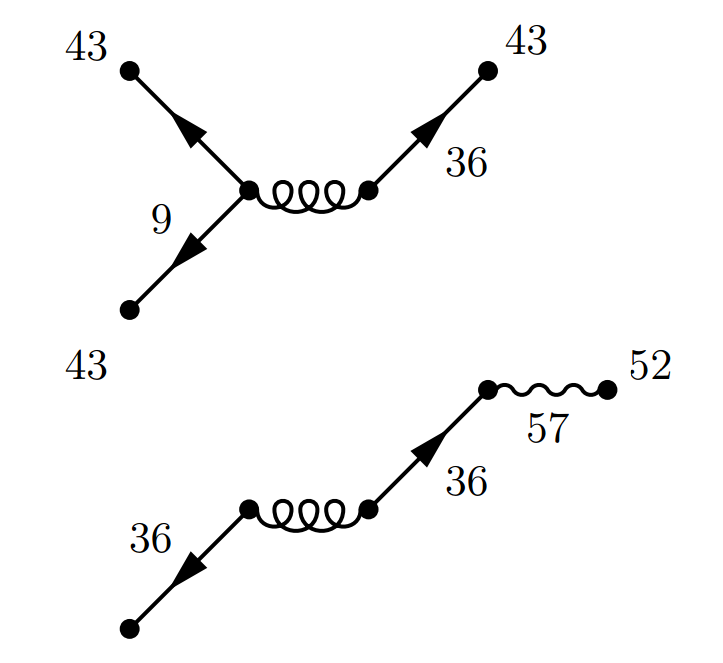
|
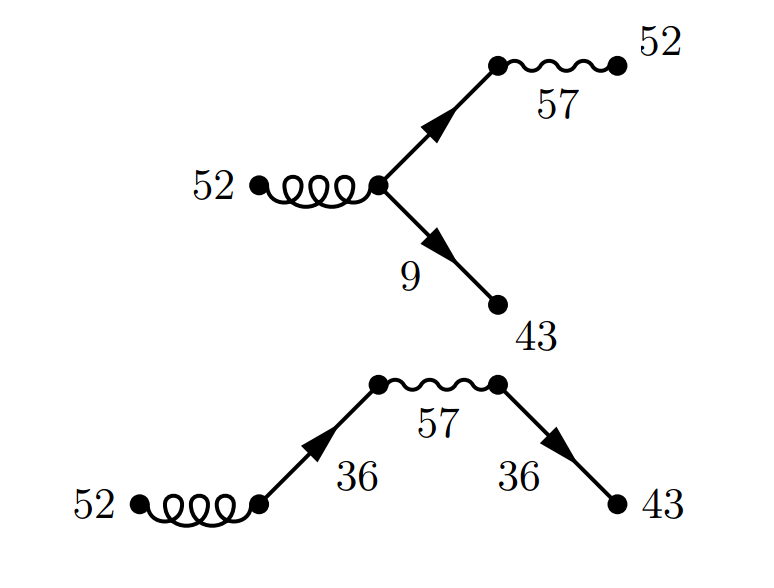
|
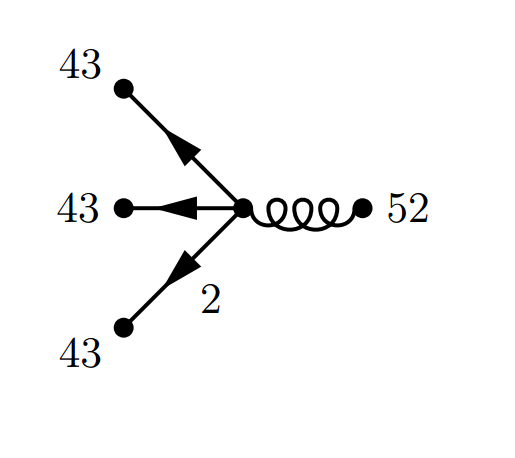
|
Zu allen obigen Konfigurationen gibt es das entsprechende Spiegelbild, so dass sich die Wahrscheinlichkeit für genau drei Gäste zu \[ 2\times 0,25\% + 2\times 2\% +2\times 0,6\% + 2\times 2\% + 2\times0.08\% = 9,86\% \] errechnet. Die Diagramme für genau vier Gäste führen wir hier nicht mehr auf. Stattdessen sei eine Tabelle wiedergegeben, die experimentell mit Hilfe eines JavaScript-Programms erstellt wurde. Das Programm erzeugt zufällig Konfigurationen unter Berücksichtigung der Wahrscheinlichkeiten für Kinderzahl und Single-Status und registriert für jede Konfiguration die Anzahl der Gäste. Das Programm findet sich ⇒ hier. Bei 1000000 Durchläufen erhält man (z.B.) folgende Werte:
| Gäste | Anteil |
| 0 | 27.03 |
| 1 | 15.72 |
| 2 | 15.19 |
| 3 | 9.58 |
| 4 | 7.86 |
| 5 | 5.42 |
| 6 | 4.22 |
| 7 | 3.13 |
| 8 | 2.42 |
| 9 | 1.88 |
| 10 | 1.46 |
| 11 | 1.13 |
| 12 | 0.91 |
Man sieht, dass die ersten Werte recht gut mit der Theorie (27%, 16%, 15.1% und 9.86%) übereinstimmen. Erstaunlich ist, dass die Brautleute im Mittel nur mit drei Gästen rechnen können! Eine Verlobungsfeier, bei der nur Personen aus der Geschwister–Partner–Kette anwesend sind, dürfte demnach eine ziemlich fade Angelegenheit werden. Man sollte unbedingt noch einige Freunde (mit den jeweiligen Partnern) einladen.