Das Möbelpacker-Problem

Die folgende Aufgabe läuft auch unter der Bezeichnung Schrankproblem. Sie wird im Netz an einigen Stellen mehr oder weniger ausführlich behandelt, etwa hier (sogar mit einer schönen Animation). Eine ähnliche Aufgabe soll bei einer Mathematik-Olympiade gestellt worden sein – leider stehen die Jahresbände nicht frei im Web, so dass ich mehr dazu nicht sagen kann.

Das hier vorgestellte Problem hat seinen Ursprung allerdings in einer konkreten Umräumaktion in unserer Wohnung. Es sollte eine Kommode von einem Zimmer in ein anderes Zimmer verschoben werden, wobei das Teil so schwer ist, dass es wirklich geschoben werden muss und nicht angehoben werden kann, um die effektive Länge zu verkürzen – in dieser Hinsicht ist es mit einem Schrank vergleichbar.

Es geht um folgendes Problem:

Genaugenommen hat der Flur 6 Ecken. Um Missverständnisse zu vermeiden, bezeichnen wir im folgenden nur die Ecke, deren Innenwinkel 270° beträgt, als die Ecke. Die anderen Ecken haben keine spezielle Bedeutung. Damit die Kommode den maximalen Abstand von der Ecke einhält, wird sie so geschoben, dass sie möglichst dicht an den der Ecke gegenüberliegenden Wänden entlang schrammt. In unserer Idealisierung bewegen sich die Kommoden-Ecken direkt an den Wänden entlang.

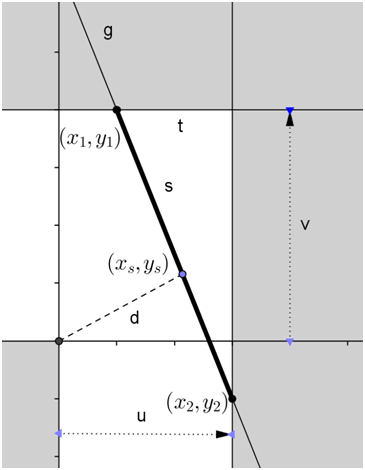
Wir legen die Flur-Ecke in den Ursprung des Koordinatensystems, dann sind die gegenüberliegenden Wände durch die achsenparallelen Geraden $x=u$ und $y=v$ gegeben. Das Problem ist somit äquivalent zu der Frage, wie groß der minimale Abstand einer Strecke der Länge $s$ vom Ursprung ist, deren Endpunkte $(x_1,y_1 )$ und $(x_2,y_2 )$ auf den Geraden $x=u$ bzw. $y=v$ liegen. Dieses Problem wird in Abb.2 veranschaulicht.

Wir parametrisieren dabei die verschiedenen Strecken (bzw. die eine Strecke in verschiedenen Positionen) durch den Abstand $t$ ihres einen Endpunkts $(x_1,y_1 )$ vom Punkt mit den Koordinaten $(u,v).$ Zunächst soll allgemein die Formel für den Abstand einer Geraden $g$ (auf der die Strecke der Länge $s$ liegt) vom Ursprung abgeleitet werden:

Die Gerade $g$ genügt der allgemeinen Geradengleichung $y=mx+c.$ Eine zu $g$ senkrechte Gerade hat die Steigung $–1/m.$ Geht diese durch den Ursprung hat sie die Gleichung $y=-1/m x.$ Wir berechnen den Schnittpunkt $(x_s,y_s )$ von $g$ mit dieser Senkrechten durch den Ursprung: $$ \begin{align*} -\frac{1}{m} x_s &= mx_s+c\\ x_s &= -\frac{m}{1+m^2} c\\ \end{align*} $$ Eingesetzt in $y_s=-\frac{1}{m} x_s$ ergibt sich $y_s=\frac{1}{1+m^2} c.$

Und damit hat man für den Abstand d nach Pythagoras: $$ d^2= x_s^2+y_s^2= \frac{m^2 c^2}{(1+m^2 )^2} +\frac{c^2}{(1+m^2 )^2} = \frac{c^2 (1+m^2 )}{(1+m^2 )^2} = \frac{c^2}{1+m^2} $$ $$ d=\frac{c}{\sqrt{1+m^2 }}\quad \quad(1) $$

Wir berechnen jetzt die Steigung und den Achsenabschnitt der Geraden $g$ unter den obigen Randbedingungen. Zunächst ist die Steigung $m$ gegeben durch $$ m= \frac{y_2-y_1}{x_2-x_1 }= -\frac{\sqrt{s^2-t^2 }}{t} $$

Der Zähler ergibt sich wieder aus dem Satz des Pythagoras, wobei das negative Vorzeichen aus der Tatsache folgt, dass $y_2 \lt y_1$ ist. Der Nenner lässt sich direkt aus der Zeichnung ablesen. Die Gerade verläuft durch den Punkt $(u-t,v),$ woraus sich der Achsenabschnitt $c$ bestimmen lässt: $$ \begin{align*} v &= m(u-t)+c\\ c &= v-m(u-t) \\ &= v+ \frac{\sqrt{s^2-t^2 }}{t} (u-t)\\ \end{align*} $$

Wir setzen die Werte für $m$ und $c$ in (1) ein und erhalten eine Gleichung für $d$ als Funktion des Parameters $t$: $$ \begin{align*} d &= \frac{c}{\sqrt{1+m^2}} = \frac{c}{\sqrt{1+\frac{s^2-t^2}{t^2}}} = \frac{ct}{s}\\ d &= (v+ \frac{\sqrt{s^2-t^2 }}{t} (u-t) )\frac{t}{s}\\ d &= \frac{vt}{s}+ \frac{\sqrt{s^2-t^2 } (u-t)}{s}\\ \end{align*} $$

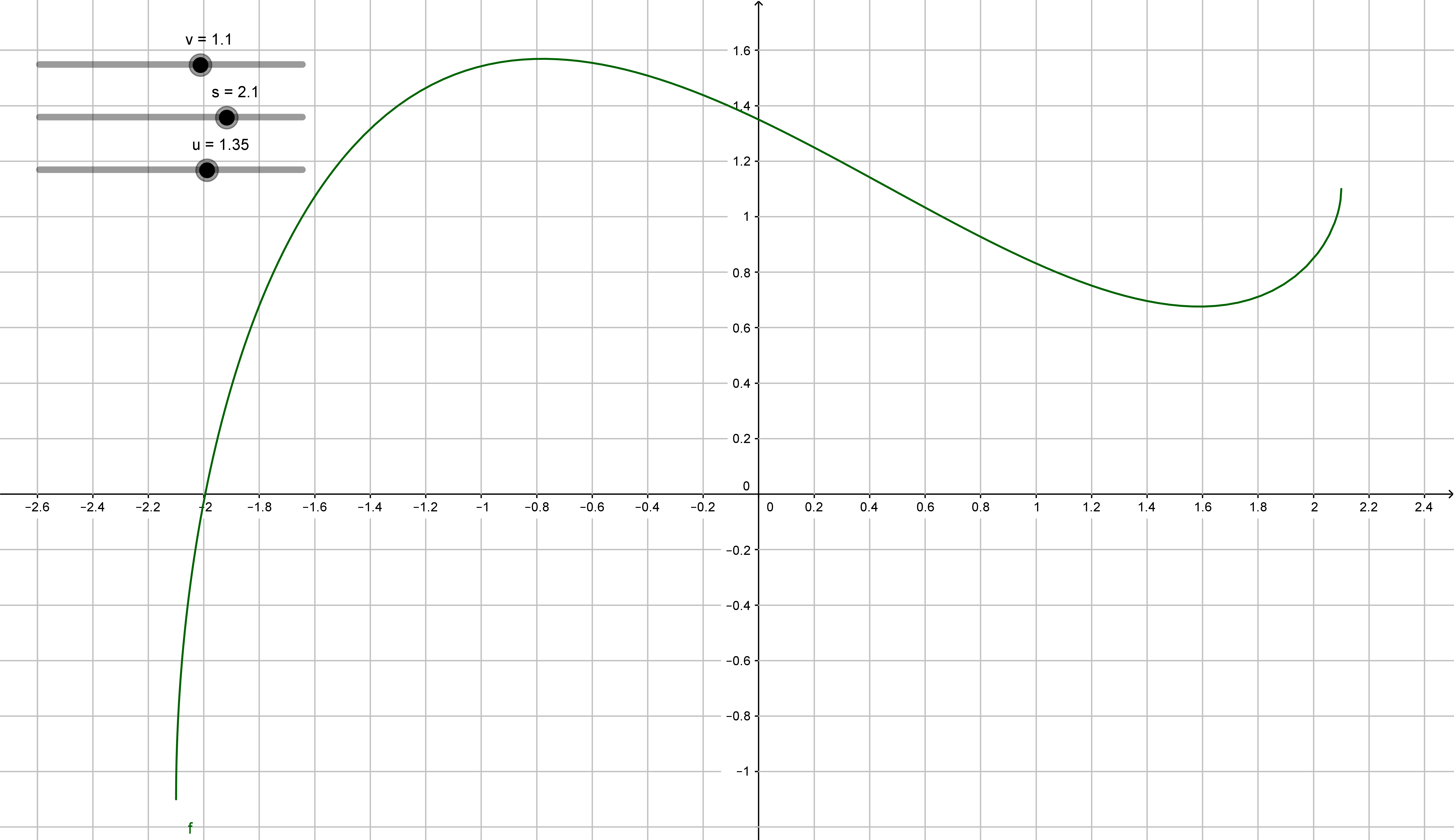
Diese Funktion lässt sich, etwa für unseren konkreten Fall $v=1.1, u=1.35, s=2.1$ (alle Maßangaben in m) mit Geogebra plotten. Man erkennt das Minimum etwa bei $1.6$ mit einem Wert von $d \approx 0.68.$ Unsere $61$cm breite Kommode passt also um die Ecke.

Man sieht, dass für $t=0$ der Wert von $d$ korrekt $1.35$ ist – die Strecke $s$ liegt hier auf der Geraden $x=u.$ Weniger aus der Grafik als aus der Formel sieht man, dass für $t=s$ der Wert $v$ angenommen wird, die Strecke $s$ liegt dann auf der Geraden $y=v.$ Für $t>s$ wird die Wurzel imaginär, der Definitionsbereich ist also $0 \le t \le s,$ negative Werte für $t$ ergeben keinen Sinn.

Um die Maxima und Minima in geschlossener Form zu bestimmen, differenzieren wir nach $t.$ Dabei benutzen wir für den zweiten Summanden sowohl die Produktregel $(fg)' = f'g+fg'$ wie auch die Kettenregel $(f(g(t))'= f' (g(t)) g' (t)$: $$ d'= \frac{1}{s}(v-\frac{t}{\sqrt{s^2-t^2 }} (u-t)-\sqrt{s^2-t^2}) $$ Setzen wir $d'(t_m )=0$ erhalten wir: $$ v-\sqrt{s^2-t_m^2 }= \frac{t_m}{\sqrt{s^2-t_m^2}} (u-t_m ) $$ Hier substituieren wir $x=\sqrt{s^2-t_m^2}$ und erhalten: $$ \begin{align*} v-x &=\frac{\sqrt{s^2-x^2 }}{x}(u-\sqrt{s^2-x^2})\\ vx-x^2 &= u\sqrt{s^2-x^2}-s^2+x^2\\ vx-2x^2+s^2 &= u\sqrt{s^2-x^2}\\ (vx-2x^2+s^2 )^2 &= u^2 (s^2-x^2 )\\ 4x^4-4vx^3+v^2 x^2-4s^2 x^2 &+ 2s^2 vx+s^4-u^2 s^2+u^2 x^2 = 0\\ 4x^4-4vx^3+(v^2-4s^2+u^2 ) x^2 &+ 2s^2 vx+s^4-u^2 s^2=0\\ \end{align*} $$

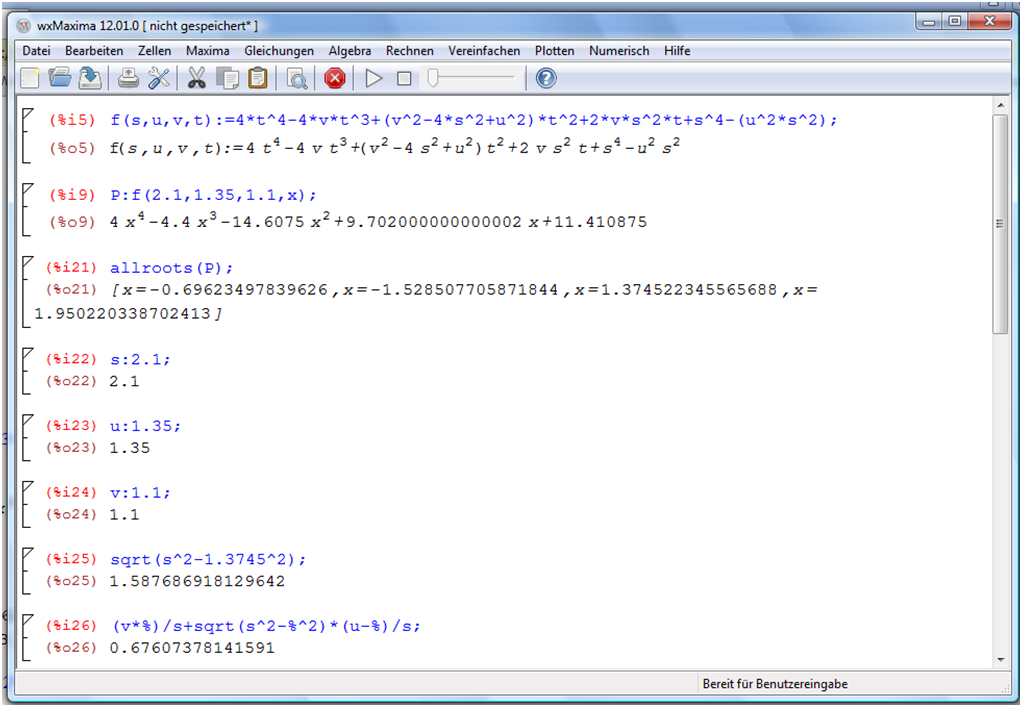
Diese Gleichung 4ten Grades lässt sich zwar in einem geschlossenen Ausdruck lösen, dieser ist jedoch so unübersichtlich, dass hier ein Näherungsverfahren angemessener erscheint, zumal man damit jedenfalls genauere Werte erhält als durch Anschauen des Plot. Für unseren speziellen Fall (Länge der Kommode $s=2.1,$ Flurbreiten $u=1.35$ und $v=1.10$) liefert wxMaxima approximativ ein Minimum bei $t_m=1.5877$ und für $d$ den Wert $0.6761,$ was mit den aus Geogebra abgelesenen Werten recht gut übereinstiimt (siehe Abb.4).

Hierbei muss man erraten, dass die 3. Nullstelle die einzig relevante ist. Wegen $0 \lt t_m \lt s$ gilt $0\lt x \lt s,$ so dass die negativen Nullstellen ignoriert werden können. Für die Nullstelle bei $x= 1.950$ ist in der oben mit %i25 gekennzeichneten Zeile der negative Wurzelwert zu nehmen und führt zum Maximum bei -0.779 mit dem Wert 1.57.

Nachdem wir wussten, dass unsere Kommode den Weg durch den Flur geschafft hätte, kamen uns Zweifel, ob das Teil an seinem neuen Ort tatsächlich so gut aussieht, wie wir das ursprünglich gedacht hatten. Fazit: Die Kommode steht immer noch an ihrem alten Platz.